April 30, 2024

Informationstheorie, Vorhersagbarkeit und die Entstehung von komplexem Leben – Luís F. Seoane, Ricard V. Solé

Axel Krauss April 12, 2024 0

Quelle: Information theory, predictability and the emergence of complex life | Royal Society Open Science

Zusammenfassung

Trotz des offensichtlichen Vorteils einfacher Lebensformen, die zu einer schnellen Replikation fähig sind, haben lebende Systeme verschiedene Stufen kognitiver Komplexität im Hinblick auf ihr Potenzial zur Bewältigung von Umweltunsicherheiten erreicht. Angesichts der unvermeidlichen Kosten, die mit der Erkennung von Hinweisen aus der Umwelt und der adaptiven Reaktion darauf verbunden sind, vermuten wir, dass das Potenzial zur Vorhersage der Umwelt die mit der Aufrechterhaltung kostspieliger, komplexer Strukturen verbundenen Kosten überwinden kann. Wir stellen ein minimales formales Modell vor, das auf der Informationstheorie und der Selektion beruht und in dem aufeinanderfolgende Generationen von Agenten als Sender und Empfänger einer kodierten Nachricht abgebildet werden. Unsere Agenten sind ratende Maschinen, und ihre Fähigkeit, mit Umgebungen unterschiedlicher Komplexität umzugehen, definiert die Bedingungen für den Erhalt komplexerer Agenten.

1. Einführung

Einfache Lebensformen dominieren unsere Biosphäre [1] und stellen eine Untergrenze verkörperter, sich selbst reproduzierender Systeme dar. Das Leben weist jedoch eine enorm große Bandbreite an Komplexitätsgraden auf, die sich auf viele verschiedene Merkmale von Lebewesen auswirken, von der Körpergröße bis zu den kognitiven Fähigkeiten [2]. Daraus ergibt sich ein gewisses Paradoxon: Wenn größere, komplexere Organismen aufwändiger zu züchten und zu erhalten sind, warum ist dann nicht alles Leben einzellig? Es gibt mehrere Argumente, mit denen sich die Entstehung und das Fortbestehen komplexer Lebensformen begründen lassen. So schlägt Gould [1] vor, dass Komplexität keine Eigenschaft ist, die von der Evolution ausdrücklich begünstigt wird. Eine Überprüfung der fossilen Aufzeichnungen überzeugt Gould davon, dass wir über Gattungen, Phyla und die gesamte Biosphäre hinweg die erwarteten zufälligen Fluktuationen um die erfolgreichsten Anpassungen an das Leben beobachten. In diesem Gesamtbild sind Bakterien die führende Lebensform, und die Komplexität jedes anderen lebenden Systems ist das Produkt einer zufälligen Drift. Komplexes Leben würde nie explizit begünstigt werden, aber es gibt eine Komplexitätsmauer direkt unter den Bakterien: einfachere Formen können nicht überleben. Daher ist es wahrscheinlicher, dass eine zufällige Fluktuation komplexere Formen hervorbringt, was fälschlicherweise suggeriert, dass die Evolution die Komplexität fördere.

Wichtige Innovationen in der Evolution sind das Auftreten neuer Arten von Agenten, die kooperieren und gleichzeitig Konflikte begrenzen [3,4]. Eine besonders wichtige Innovation war das Aufkommen kognitiver Agenten, d. h. von Agenten, die in der Lage sind, ihre Umgebung wahrzunehmen und auf deren Veränderungen in höchst anpassungsfähiger Weise zu reagieren [5]. Diese Agenten waren in der Lage, mit komplexeren, nicht-genetischen Formen von Informationen umzugehen. Die Vorteile einer solchen kognitiven Komplexität werden deutlich, wenn man bedenkt, dass sie in der Lage sind, die Umwelt besser vorherzusagen und damit die durchschnittlichen Risiken unerwarteter Schwankungen zu verringern. Wie Francois Jacob betont, ist ein Organismus „eine Art Maschine zur Vorhersage der Zukunft – ein automatischer Prognoseapparat“ ([6], S. 9; siehe auch [7,8]). Die Hauptaussage ist, dass die Vorhersage der Zukunft eine entscheidende Fähigkeit ist, um mit Ungewissheit umzugehen. Wenn die Vorteile der Vorhersage das Problem der Aufrechterhaltung und Replikation der kostspieligen Strukturen, die für die Inferenz erforderlich sind, überwinden, könnten komplexere Informationsverarbeitungsmechanismen unter den entsprechenden Umständen bevorzugt werden.

Diese Art von Problem wurde im Rahmen ökologischer und evolutionärer Perspektiven behandelt. Ein besonders interessantes Problem betrifft das Potenzial einiger Arten von Organismen, ein kognitives Potenzial für Vorhersagen zu entwickeln. Sind alle lebenden Systeme in der Lage, eine solche Eigenschaft zu entwickeln? Wo liegt die Grenze der Vorhersagekraft für eine bestimmte Gruppe, und wie wird sie durch die Lebensweise beeinflusst? Pflanzen zum Beispiel haben kein Nervensystem, weisen aber einige interessante Fähigkeiten zur Entscheidungsfindung, zur Unterscheidung von Selbst und Nicht-Selbst oder zur Fehlerkorrektur auf [9]. Studien, die sich mit der Evolution der Vorhersage bei simulierten Pflanzen befassen, zeigen, dass eine bessere Vorhersagbarkeit der verfügbaren Ressourcen durch eine angemessene Bewertung der Umweltvariabilität erreicht wurde [10]. Einige der molekularen Mechanismen, die die Reaktionen von Pflanzen durchdringen, scheinen mit schalterähnlichen Veränderungen zu tun zu haben, die durch genetische Netzwerke ausgelöst werden [11]. In diesem Fall korrelieren Wachstum, Samenproduktion oder Keimung mit dem Ausmaß der Umweltschwankungen. Eine wichtige Schlussfolgerung, die für unsere Arbeit von Bedeutung ist, lautet, dass einige Reproduktionsstrategien in bestimmten Umgebungen aufgrund mangelnder Vorhersagbarkeit nicht ausgewählt werden.

Unser Ziel ist es, ein minimales Modell zu erstellen, das diese Kompromisse erfasst. Auf diese Weise charakterisieren wir gründlich einen evolutionären Antrieb, der zu immer komplexeren Lebensformen führen kann. Wir nehmen eine informationstheoretische Perspektive ein, in der Agenten Inferenzgeräte sind, die mit einer booleschen Umgebung interagieren. Der Einfachheit halber wird diese Umgebung durch ein Band mit Einsen und Nullen dargestellt, ähnlich wie die nicht leeren Eingänge einer Turing-Maschine (Abbildung 1a). Der Agent G befindet sich an einer gegebenen Position und versucht, jedes Bit einer gegebenen Sequenz der Länge n vorherzusagen, weshalb er auch als n-Schätzer bezeichnet wird [im Englischen Original „guesser“, also auf Deutsch „Rater“ oder „Ratespieler“. Da es hier um die Fähigkeit geht, Ergebnisse bestimmter Prozesse des Informationsaustausches abzuschätzen, und dadurch auf die Entwicklung eines Organismus Einfluss zu nehmen, bleibe ich durch den Artikel bei „Schätzer“, Anm. d. Übersetzers]. Jeder Versuch, ein Bit vorherzusagen, ist mit gewissen Kosten c verbunden, während er für jede erfolgreiche Vorhersage eine Belohnung r erhält. 1-Schätzer sind einfach und gehen davon aus, dass alle Bits unkorreliert sind, während (n>1)-Schätzer Korrelationen finden und einen größeren Nutzen erzielen können, wenn in der Umgebung zufällig eine Struktur vorhanden ist. Ein ganzer n-Bit-Vorhersagezyklus kann als Programm beschrieben werden (Abbildung 1b). Eine Überlebensfunktion ρ hängt von der Anzahl der Versuche, Bits zu erraten, und der Anzahl der richtigen Vorhersagen ab. Erfolgreiche Schätzer haben ein positives Gleichgewicht zwischen Belohnung und Vorhersagekosten. Sie werden repliziert und geben ihre Inferenzfähigkeiten weiter. Andernfalls gelingt es dem Agenten nicht, sich zu vermehren, und er stirbt schließlich.

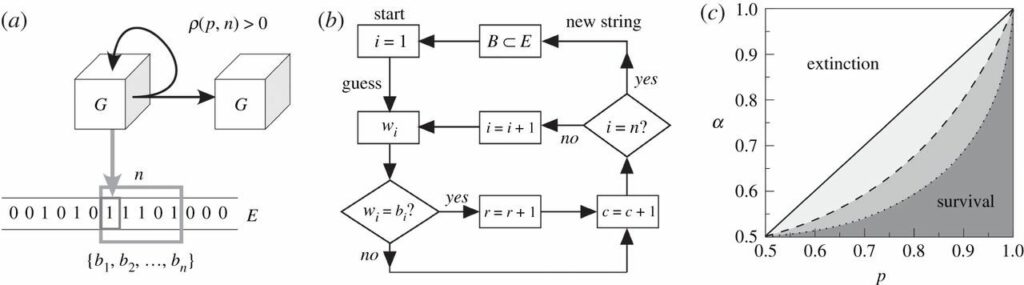
Abbildung 1. Prädiktive Agenten und Umweltkomplexität. (a) Ein Agent G interagiert mit einer externen Umgebung E, die als eine Kette von Zufallsbits modelliert ist. Diese Bits nehmen mit der Wahrscheinlichkeit p den Wert 0 an, ansonsten den Wert 1. Der Agent versucht, eine Folge von n Bits zu erraten, was mit gewissen Kosten verbunden ist, wobei für jedes richtig erratene Bit eine Belohnung gewährt wird. Das Fortbestehen und die Vervielfältigung des Agenten können nur gewährt werden, wenn das Gleichgewicht zwischen Belohnung und Kosten positiv ist (\( \rho^{G}_{E} > 0 \) ). (b) Für eine Maschine, die versucht, n Bits zu erraten, wird eine algorithmische Beschreibung ihres Verhaltens in Form eines Flussgraphen dargestellt. Jede Schleife in der Berechnung beinhaltet das Scannen einer zufälligen Teilmenge der Umgebung B=(b1…,bn)⊂E durch Vergleich jedes bi∈B mit einem vorgeschlagenen Schätzwert wi. (c) Ein Mean-Field-Ansatz für eine bestimmte Art von 1-Schätzern (im Text durch die Gleichungen (1.1)-(1.3) modelliert) in Umgebungen unendlicher Größe ergibt eine Grenze zwischen Überleben (\( \rho^{G}_{E} > 0 \)) und Tod (\( \rho^{G}_{E} < 0 \)) als Funktion des Kosten-Belohnungs-Verhältnisses (α) und der relevanten Parameter für das 1-Schätzer-Modell (in diesem Fall p).

Zur einfachen Veranschaulichung unseres Ansatzes betrachten wir einen 1-Schätzer, der in einer unendlich großen Umgebung E lebt, in der unkorrelierte Bits den Wert 1 mit der Wahrscheinlichkeit p und 0 mit der Wahrscheinlichkeit 1-p annehmen. Die durchschnittliche Leistung eines Schätzers G bei dem Versuch, Bits aus E abzuleiten, ist durch (\( p^{-G}_{E} \) ) gegeben, d. h. die Wahrscheinlichkeit, einen richtigen Tipp abzugeben:

\( p^{-G}_{E} = p^G(1)p + p^G(0)(1-p), \qquad \) 1.1

wobei pG(k) die Häufigkeit ist, mit der der Schätzer den Bitwert k∈{0,1} aussendet. Die bestmögliche Strategie besteht darin, immer das am häufigsten vorkommende Bit in der Umgebung auszusenden. Dann gilt

\( p^{-G}_{E} = max \{p,1 – p\}. \qquad \qquad \enspace \enspace \enspace \enspace\) 1.2

Nehmen wir ohne Verlust der Allgemeinheit an, dass 1 das häufigste Bit ist. Dann lautet die durchschnittliche Belohnung minus Kosten, die ein solcher Schätzer erhält:

\( \rho^{G}_{E} = pr-c = (p-\alpha). \qquad \qquad \enspace \enspace \) 1.3

Diese Kurve diktiert trivialerweise das durchschnittliche Überleben oder Aussterben der optimalen 1-Schätzer in unendlichen, unstrukturierten Umgebungen als Funktion des Kosten-Belohnungs-Verhältnisses α≡c/r (grauer Bereich, der von der durchgezogenen diagonalen Linie in Abbildung 1c begrenzt wird). Man beachte, dass dieser Parameter α die Schwere der Umgebung kodiert, d. h. wie viel eine Belohnung angesichts der dafür erforderlichen Investition wert ist. Außerdem ist zu beachten, dass komplexere Schätzer (wie die in den folgenden Abschnitten beschriebenen) in diesem Fall immer am schlechtesten abschneiden würden: Sie würden potenziell höhere Kosten zahlen, um auf eine Struktur zu schließen, wo es keine gibt. Dies führt zu engeren Überlebensbereichen, die qualitativ durch die Grautöne der unterbrochenen Linien in Abbildung 1c dargestellt werden. Auch hier würden diese reduzierten Nischen für komplexere Bit-Schätzer zustande kommen, weil es keine Struktur abzuleiten gibt; aber das kann sich ändern, wenn Korrelationen zwischen Umweltbits auftreten, wie wir weiter unten sehen werden.

Die Idee der Autonomie und die Tatsache, dass die Vorhersage der Zukunft eine Art von Berechnung voraussetzt, legen nahe, dass eine schlüssige Theorie der Komplexität des Lebens reproduzierende Individuen (und schließlich Populationen) und Informationen (sie müssen in der Lage sein, zukünftige Umweltzustände vorherzusagen) einbeziehen muss. Diese beiden Komponenten stellen einen Konflikt und einen evolutionären Zielkonflikt dar. Zu einfach zu sein bedeutet, dass die Außenwelt als eine Quelle von Rauschen wahrgenommen wird. Unerwartete Schwankungen können schädlich sein, und nützliche Strukturen können nicht zu Ihrem Vorteil genutzt werden. Wenn wir komplexer werden (und damit in der Lage sind, größere Strukturen abzuleiten, falls es sie gibt), besteht das Risiko, dass wir nicht genug Energie sammeln können, um die Mechanismen für die Ableitung zu unterstützen und zu reproduzieren. Wie weiter unten gezeigt wird, ist es möglich, die kritischen Bedingungen für das Überleben als Funktion der Komplexität des Agenten abzuleiten und diese Bedingungen mit der Informationstheorie zu verbinden. Wie oben dargelegt, können wir auf diese Weise ein Szenario mathematisch charakterisieren, in dem die Komplexität eines Schätzers explizit ausgewählt wird. Tatsächliche Lebewesen werden die notwendigen Inferenzmechanismen in ihrer Morphologie oder in ihren genetischen oder neuronalen Netzen verkörpern. Anstatt spezifische Modelle für jede dieser alternativen Implementierungen zu entwickeln, greifen wir auf mathematische Abstraktionen zurück, die auf Bit-Strings basieren und deren Schlussfolgerungen allgemein sind und für jede gewählte Strategie gelten.

2. Evolution und Informationstheorie

Schlüsselaspekte der Informationstheorie stehen in engem Zusammenhang mit Formulierungen aus der statistischen Physik [12-14], und es gab mehrere Aufrufe, die Informationstheorie stärker in die biologische Forschung zu integrieren [15-23]. Diese Theorie soll unter anderem in der Populations- oder Ökosystemdynamik, in der regulatorischen Genomik und in der chemischen Signalverarbeitung eine wichtige Rolle spielen [7,24-41], aber ein vereinheitlichender Ansatz ist noch lange nicht erreicht. Aufgrund ihrer Allgemeingültigkeit und Leistungsfähigkeit wurde die Informationstheorie auch zur Lösung von Problemen herangezogen, die eine Verbindung zwischen der darwinistischen Evolution und der Thermodynamik fernab des Gleichgewichts herstellen [42-46]. In ihrer ursprünglichen Formulierung betrachtet die Informationstheorie von Shannon [47,48] die Übertragung von Symbolen von einem Sender zu einem Empfänger über einen Kanal. Shannon befasst sich nur mit der Effizienz des Kanals (bezogen auf sein Rauschen oder seine Zuverlässigkeit) und der Entropie der Quelle. Diese Theorie ignoriert den Inhalt der gesendeten Symbole, obwohl eine solche Annahme nur begrenzt möglich ist [18,49].

Eine zufriedenstellende Verbindung zwischen natürlicher Selektion und Informationstheorie lässt sich herstellen, indem wir unsere Überlebensfunktion ρ in Shannons Sender-Empfänger-Schema abbilden. Dazu betrachten wir Replikatoren in einer beliebigen Generation T, die versuchen, eine Nachricht an eine spätere Generation T+1 zu „senden“ (d. h. in diese repliziert zu werden). Die ältere Generation fungiert also als Sender, die jüngere wird zum Empfänger, und die Umwelt und ihre Zufälligkeiten stellen den Kanal dar, durch den die verkörperte Botschaft übermittelt werden muss (Abbildung 2a). Aus einer eher biologischen Perspektive können wir uns einen Genotyp als ein generatives Modell (die Anweisungen in einem Algorithmus) vorstellen, das eine Botschaft produziert, die übermittelt werden muss. Diese Botschaft wird durch einen Phänotyp verkörpert und umfasst alle physikalischen Prozesse und Strukturen, die durch das generative Modell vorgegeben werden. Wie von Neuman & Burks [50] erörtert, muss jede sich replizierende Maschine eine physisch verkörperte Kopie ihrer Anweisungen weitergeben – daher muss der Phänotyp auch eine physische Realisierung des vom Genotyp kodierten Algorithmus enthalten.1 Schließlich kann jeder evolutionäre Druck (einschließlich der Interaktion mit anderen replizierenden Signalen) als Mittel des Kanals einbezogen werden.

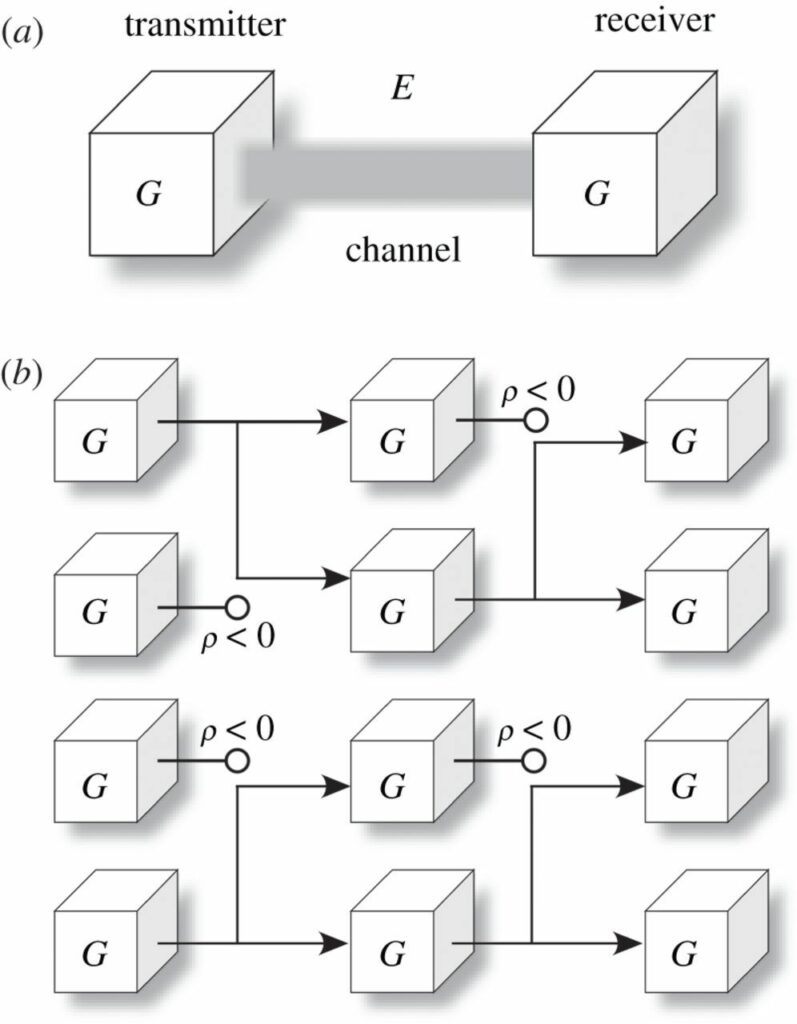
Abbildung 2. Information und Evolution durch natürliche Selektion. (a) Die Ausbreitung eines erfolgreichen Replikators kann als Shannon-ähnlicher Übertragungsprozess von einer Generation zur nächsten verstanden werden, bei dem ältere Generationen die Rolle eines Senders und jüngere Generationen die eines Empfängers spielen und die Umwelt einen verrauschten Kanal darstellt. (b) Ein einfaches Diagramm der zugrundeliegenden Entwicklung einer Population von Bit-Schätzers. Das Überleben und die Replikation eines bestimmten Agenten G wird durch Verzweigungen angezeigt, während das Nicht-Überleben durch einen leeren Kreis als Endpunkt dargestellt wird.

Maynard-Smith [18] schlägt in Anlehnung an eine ähnliche Idee der Weitergabe von Nachrichten von einer Generation zur nächsten vor, dass die replizierte genetische Nachricht bedeutungsvolle Informationen enthält, die gegen die Zufälligkeiten des Kanals geschützt werden müssen. Gehen wir stattdessen von einer replizierenden Nachricht ohne Bedeutung aus. Wir stellen fest, dass der Kanal selbst die Botschaften zuverlässiger übermitteln würde, die durch einen Phänotyp verkörpert werden, der besser mit den Umweltbedingungen (d. h. dem Kanal) zurechtkommt. Dysfunktionale Botschaften werden durch die natürliche Selektion entfernt. Effiziente Signale erhalten in nachfolgenden Generationen mehr Platz (Abbildung 2b). Durch diesen Prozess werden aussagekräftige Informationen aus der Umwelt in die sich replizierenden Signale gepumpt, so dass die Informationen in künftigen Nachrichten diese Kanalbedingungen vorwegnehmen. In unserem Bild ist die bedeutungsvolle Information nicht vor den Kanalbedingungen (einschließlich Rauschen) geschützt, sondern ergibt sich ganz natürlich aus ihnen.

2.1 Nachrichten, Kanäle und Bit-Schätzer

Zunächst wollen wir unsere Implementierung von Umgebungen (Kanälen), Nachrichten und den sich replizierenden Agenten vorstellen. Letztere werden als Bit-Schätzer bezeichnet, da eine effiziente Übertragung gleichbedeutend mit einer genauen Vorhersage der Kanalbedingungen ist, d. h. mit dem korrekten Erraten möglichst vieler Bits der Umgebung. Die folgende Notation mag trocken erscheinen, daher ist es gut, ein zentrales Bild beizubehalten (Abbildung 3): Schätzer G besitzen ein generatives Modell ΓG, das Nachrichten produzieren muss, die in einer Umgebung E gut funktionieren. Es folgt eine strenge mathematische Beschreibung, wie die verschiedenen Bitfolgen erzeugt werden.

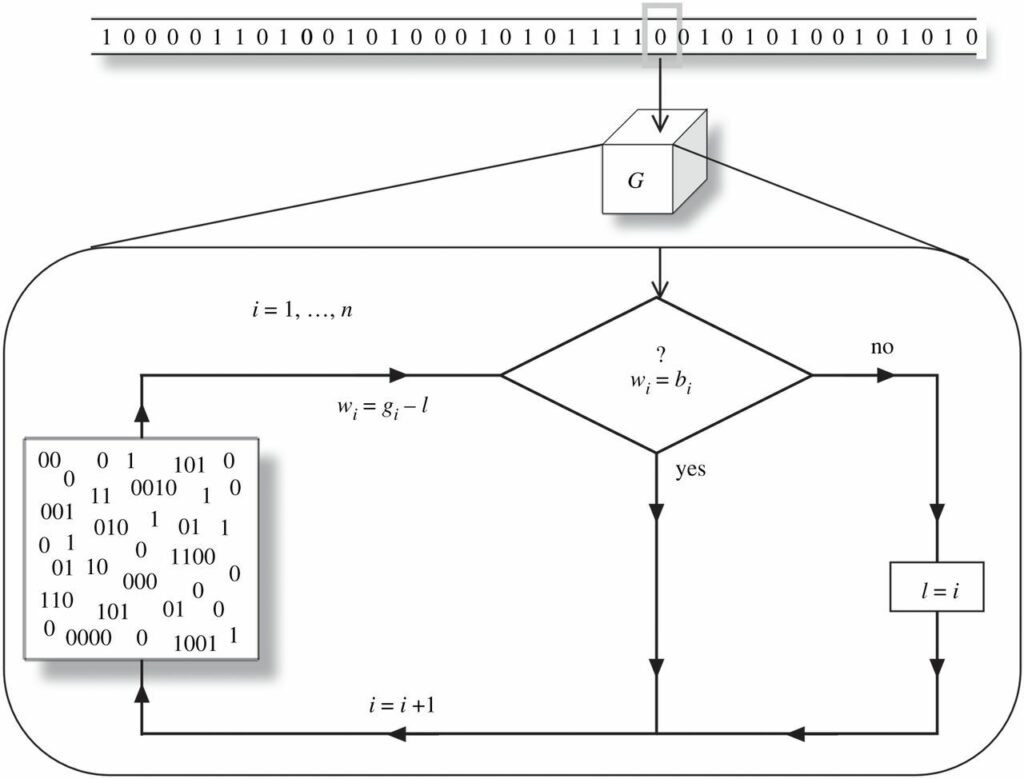
Abbildung 3. Von einem generativen Modell zu Schlussfolgerungen über die Welt. Eine schematische Darstellung der algorithmischen Logik der Bit-Ratemaschine. Unser n-Schätzer enthält ein generatives Modell (dargestellt durch einen Pool von Wörtern), aus dem er Vermutungen über die Umgebung ableitet. Wird ein Bit erfolgreich abgeleitet, wird die gewählte Vermutung durch den Vergleich eines neuen Bits weiterverfolgt. Andernfalls wird die Schlussfolgerung zurückgesetzt.

Betrachten wir m-Umgebungen, Zeichenketten, die aus m sortierten Zufallsbits bestehen. Wir könnten eine einzige solche m-Umgebung betrachten, d.h. eine Realisierung E von m sortierten Zufallsbits (ei ∈ E, i=1,…,m; ei ∈ {0,1}). Alternativ könnten wir mit dem Ensemble Em aller m-Umgebungen arbeiten – d.h. allen möglichen Umgebungen der gleichen Größe (ei,l ∈ El, i=1,…,m; wobei El∈Em, l=1,…,2m)- oder wir könnten mit einer Stichprobe Êmdieses Ensembles arbeiten: El ∈ Êm, l = 1,…, ‖Êm‖; wobei Êm ⊂ Em. Wir können die Leistung unserer Bit-Schätzer in einzelnen m-Umgebungen, in einem ganzen Ensemble oder in einer Stichprobe davon bewerten.

Diese m-Umgebungen stellen die Kanäle unseres informationstheoretischen Ansatzes dar. Der Versuch, eine Nachricht über diesen Kanal zu übermitteln, wird dadurch realisiert, dass versucht wird, Wörter der Größe n aus der entsprechenden m-Umgebung zu erraten. Genauer gesagt: Bei einer n-Bit-Nachricht W (mit n<m), die ein Agent zu übermitteln versucht, extrahieren wir ein Wort der Größe n (B ⊂ E) aus der entsprechenden m-Umgebung. Dazu wählen wir ein Bit an einer zufälligen Position in E und die darauf folgenden n-1 Bits. Diese bilden das bi ∈ B, das mit dem wi ∈ W verglichen wird. Jedes wi wird erfolgreich über den Kanal übertragen, wenn wi = bi. Der Versuch, Nachrichten zu übermitteln, wird somit zu einer Inferenzaufgabe: Wenn ein Schätzer die folgenden Bits vorhersehen kann, hat er eine größere Chance, Nachrichten zu übermitteln. Übermittelte Nachrichten entsprechen Bits, die in eine spätere Generation kopiert werden, wodurch sich die Fitness des Agenten erhöht.

In dieser Arbeit erlauben wir Bit-Schätzern eine minimale Fähigkeit, auf die Umgebung zu reagieren. Anstatt zu versuchen, ein festes Wort W zu übermitteln, werden sie mit einem generativen Modell ΓG ausgestattet. Dieser Mechanismus (der weiter unten erläutert wird) baut die Nachricht W als Funktion der Übertragungshistorie auf:

wi = wi(w1,…,wi-1 ; b1,…,bi-1).

Daher basiert die Eignung eines generativen Modells eher auf der Gesamtheit der Nachrichten, die es produzieren kann.2 Um dies zu bewerten, versuchen unsere Schätzer, n-Bit-Wörter viele (Ng) Male über denselben Kanal zu übertragen.

Für jede dieser Übertragungen wird ein neues n-großes Wort Bj⊂ E (mit \( b^{i}_{j} \) ∈ Bj für j=1,…,Ng und i=1,…,n) aus derselben m-Umgebung extrahiert; und die entsprechenden Wj werden generiert, jeweils auf der Grundlage der Sendegeschichte, wie sie vom generativen Modell vorgegeben wird (siehe unten).

Wir können verschiedene Häufigkeiten berechnen, mit denen die Schätzer oder die Umgebung Bits mit dem Wert k,k′ ∈ {0,1} präsentieren:

\( p^{G}(k;i) = \frac{1}{N_g}\sum_{j=1}^{N_g}\delta(w^{j}_{i}, k), \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.1

\( p_{E}(k‘;i) = \frac{1}{N_g}\sum_{j=1}^{N_g}\delta(b^{j}_{i}, k‘), \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.2

\( p_{G,E}(k, k‘;i) = \frac{1}{N_g}\sum_{j=1}^{N_g}\delta(w^{j}_{i}, k)\delta(b^{j}_{i}, k‘), \qquad \) 2.3

\( p^{G}_{E}(i) = \frac{1}{N_g}\sum_{j=1}^{N_g}\delta(w^{j}_{i}, b^{j}_{i}) \Rightarrow \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.4

und \( \enspace \enspace \enspace \Rightarrow p^{-G}_{E} = \frac{1}{n}\sum_{i=1}^{n}p^{G}_{E}(i); \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.5

wobei δ(x,y) das Dirac-Delta ist. Man beachte, dass pG(k;i) eine subtile Abhängigkeit von der Umgebung hat (weil G auf sie reagieren kann) und dass die durchschnittliche Wahrscheinlichkeit \( p^{G}_{E} \) angibt, dass der Schätzer G erfolgreich ein Bit über den Kanal E sendet.

Dank dieser Gleichungen können wir eine Verbindung zu den zuvor eingeführten Kosten- und Belohnungsfunktionen herstellen. Für jedes Bit, das zu übertragen versucht wird, wird ein Preis c gezahlt. Eine Belohnung r=c/α wird nur dann ausgezahlt, wenn das Bit erfolgreich empfangen wird. α ist ein Parameter, der die Auszahlung kontrolliert. Die Überlebensfunktion lautet

\( \rho^{G}_{E}(\alpha) = (p^{-G}_{E} – \alpha)r \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.6

und \( p^{-G}_{E} \) kann aus Gleichung (2.5) abgelesen werden. Als Faustregel gilt: Wenn \( p^{-G}_{E} > \alpha \), schneidet der gegebene Schätzer in der vorgeschlagenen Umgebung gut genug ab.

Es ist nützlich, die Entropie pro Bit der von G erzeugten Nachrichten zu quantifizieren:

\( H(G) = -\frac{1}{n}\sum_{i=1}^{n}\sum_{k}p^{G}(k;i)log(p^{G}(k;i)) \enspace \enspace \enspace \) 2.7

und die gegenseitige Information zwischen den Nachrichten und der Umwelt:

\( I(G:E) = \frac{1}{n}\sum_{i=1}^{n}\sum_{k,k‘}p_{G,E}(k,k‘;i) \times log(\frac{p{G,E}(k,k‘;i)}{p^{G}(k;i)p_{E}(k‘;i)}) \qquad \) 2.8

Um die Leistung eines Schätzers über ein Ensemble Êm von Umgebungen (statt über einzelne Umgebungen) zu bewerten, versuchen wir, Ng-Sendungen über jede von Ne verschiedenen Umgebungen (El ∈ Êm, l = 1,…,Ne ≡ ‖Êm‖) einer bestimmten Größe. Der Einfachheit halber stapeln wir alle Ng×Ne n-großen Wörter Wj und Bj zusammen, anstatt \( b^{j}_{i,l} \) zu beschriften. Auf diese Weise sind \( b^{j}_{i} \) ∈ Bj und \( w^{j}_{i} \) ∈ Wj für i=1,…,n und j=1,…,NgNe. Wir haben pG(k;i), \( p_{Ê^{m}}(k‘;i)\), \( p_{G,Ê^{m}}(k,k‘;i) \), \( p^{G}_{Ê^{m}}(i) \) und \( p^{-G}_{Ê^{m}} \) genau wie in den Gleichungen (2.2)-(2.5) definiert, nur dass j durch j=1,…,NgNe läuft. Auch hier wird die Auszahlung über die Umgebungen hinweg gemittelt, um zu bestimmen, ob die Nachrichten eines Schätzers erfolgreich übermittelt werden oder nicht, wenn α und die Länge m der Umgebungen im Ensemble gegeben sind durch

\( \rho^{G}_{Ê^{m}}(\alpha) = (p^{-G}_{Ê^{m}} – \alpha)r. \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.9

Beachten Sie, dass sich

\( I(G:Ê^{m}) = \frac{1}{n}\sum_{i=1}^{n}\sum_{k,k‘}p_{G,Ê^{m}}(k,k‘;i) \times log(\frac{p_{G,Ê^{m}}(k,k‘;i)}{p^{G}(k;i)p_{Ê^{m}}(k‘;i)}) \qquad \) 2.10

unterscheidet von

\( \langle I(G:E)\rangle_{Ê^{m}} = \frac{1}{N_{e}} \sum_{l=1}^{N_{e}}I(G:E_{l}). \qquad \enspace \enspace \enspace \enspace \enspace \) 2.11

Wir verwenden den Begriff \( \langle.\rangle_{Ê^{m}} \), um Durchschnittswerte über die Umgebungen eines Ensembles Êm anzugeben.

Schließlich erörtern wir die generativen Modelle, die den Kern unserer Bit-Schätzer bilden. Dabei handelt es sich um Mechanismen, die n-große Bitfolgen erzeugen, teilweise als Reaktion auf Zufälligkeiten der Umgebung. Solche nachrichtengenerierenden Prozesse ΓG können auf unterschiedliche Weise implementiert werden, darunter künstliche neuronale Netze (ANNs) [51], Spiking Neurons [52], Bayes’sche Netze [53,54], Turing-Maschinen [55], Markov’sche Ketten [56], ϵ-Maschinen [57], zufällige boolesche Netze (RBNs) [58] und andere. Diese Geräte entwickeln ihre Vermutungen durch eine Reihe von Algorithmen (z. B. Backpropagation, Message Passing oder Hebbian Learning), sofern sie Zugang zu einer Stichprobe ihrer Umgebung haben.

In der realen Welt wären Versuch und Irrtum und die Evolution durch natürliche Auslese der Algorithmus, der das ΓG (oder, in einer biologischeren Sprache, einen Genotyp) in unsere Agenten verdrahtet. Die Dynamik eines solchen evolutionären Prozesses ist sehr interessant. In dieser Arbeit geht es jedoch darum, die Grenzen zu verstehen, die durch die Komplexität eines Kanals und die Kosten der Inferenz gesetzt werden, und nicht um die Dynamik, wie diese Grenzen erreicht werden können. Daher gehen wir davon aus, dass unsere Agenten angesichts der Umgebung, in der sie leben, eine nahezu perfekte Inferenz durchführen. Diese beste Inferenz wird im generativen Modell ΓG des Schätzers fest verdrahtet, wie weiter oben erläutert.

Das generative Modell eines Schätzers hängt in der Regel von der Umgebung ab, in der er eingesetzt wird, also stellen wir fest \( \Gamma^{G} \) ≡ \( \Gamma^{G}_{E} \) . Dieses \( \Gamma^{G}_{E} \) besteht aus einem Pool von Bits \( g_{i} \) ∈ \( \Gamma^{G}_{E} \) (Abbildung 3) und einer Reihe von Regeln, die vorschreiben, wie diese Bits zu senden sind: entweder in einer vorgegebenen Reihenfolge oder als Reaktion auf die sich ändernden Bedingungen des Kanals. Wann immer wir eine Umgebung E={ei,i=1,…,m} aufnehmen, wird das Bit (0 oder 1), das am häufigsten auftaucht, die bestmögliche erste Vermutung sein. Daraus folgt:

\( \Gamma^{G}_{E}(1) \) ≡ \( g_{1} = max_{k‘} \{p_{E}(k‘;1)\}. \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.12

Wenn sowohl 0 als auch 1 gleich häufig vorkommen, wählen wir ohne Verlust der Allgemeinheit 1. Gelingt dem Agenten die erste Vermutung, so ist es am sichersten, wenn er das Bit (0 oder 1) aussendet, das in der Umgebung häufiger auf g1 folgt. Ähnlich verfahren wir, wenn die ersten beiden Bits richtig erraten wurden, wenn die ersten drei Bits richtig erraten wurden usw. Wir definieren pB|Γ(k;i) als die Wahrscheinlichkeit, k={0,1} an der i-ten Position des aus der Umgebung extrahierten Wortes Bj zu finden, vorausgesetzt, die bisherige Vermutung ist richtig:

\( p_{B|\Gamma}(k‘;i) = \frac{1}{Z(i)}\sum_{j=1}^{m}\delta(b^{j}_{i}, k‘) \prod^{i-1}_{i’=1} \delta(b^{j}_{i}, g_{i‘}). \qquad \enspace \enspace \enspace \enspace \enspace \) 2.13

Der Index j bezeichnet in diesem Fall alle Wörter der Größe n in der Umgebung (\( b^{j}_{i} \) ∈ Bj ) \( \subset \) E und Z(i) ist eine Normalisierungskonstante, die davon abhängt, wie viele Wörter in der Umgebung mit \( \Gamma^{G}_{E} \) bis zum (i-1)-ten Bit übereinstimmen:

\( Z(i) = \sum_{j=1}^{m} \prod_{i’=1}^{i-1} \delta(b^{j}_{i‘}, g_{i‘}). \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.14

Daraus folgt:

\( \Gamma^{G}_{E}(i=2,…,n) \) ≡ \( g_{i} = max_{k‘} \{p_{B|\Gamma}(k‘;i)\}. \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.15

Man beachte, dass der Pool von Bits in \( \Gamma^{G}_{E} \) aus einem n-großen Wort besteht, das sie über den Kanal zu senden versuchen (d.h. es stellt die Vermutung über den Kanal dar). Wäre ein Schätzer nicht in der Lage, auf Umgebungsbedingungen zu reagieren, wäre das Wort W, das tatsächlich bei jeder Aussendung erzeugt wird, in jedem Fall und bei \( w^{j}_{i} = g_{i} \) immer gleich; wir erlauben unseren Schätzern jedoch eine minimale Reaktion, wenn eines der Bits nicht durchkommt (d. h. wenn eine der Vermutungen nicht korrekt ist). Diese minimale Reaktionsfähigkeit unserer Schätzer ergibt sich aus:

\( w^{j}_{i} = \Gamma^{G}_{E}(i-l) = g_{i-l} \qquad \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \enspace \) 2.16

wobei l das größte i ist, bei dem \( w^{j}_{i]} \neq b^{j}_{i} \). Das bedeutet, dass ein Schätzer die Übertragung immer dann neu startet, wenn er einen Fehler macht.3

Insgesamt besteht unser Schätzer aus einem generativen Modell ΓG, das einen Pool von Bits und eine einfache bedingte Anweisung enthält. Dies spiegelt sich in dem Flussdiagramm in Abbildung 3 wider.

Wir haben eine Reihe von Entscheidungen getroffen, wie die Umgebungsbedingungen implementiert werden sollen. Diese Entscheidungen wirken sich darauf aus, wie ein gewisses Maß an Zufälligkeit in das Modell einfließt (was sich in der Tatsache widerspiegelt, dass ein Schätzer in einer Umgebung E auf verschiedene Wörter Bj ⊂ E stoßen kann) und auch darauf, wie wir unsere Schätzer implementieren (einschließlich ihrer minimalen Anpassungsfähigkeit an falsche Ratschläge). Wir haben uns ein Schema ausgedacht, das Schätzer, Umgebungen (oder Kanäle) und Nachrichten als Bit-Strings kodiert. Dies ermöglicht uns eine direkte Messung von informationstheoretischen Merkmalen, die für unsere Diskussion geeignet sind, aber die Schlussfolgerungen, zu denen wir kommen, sollten allgemein sein. Das Überleben hängt von der Fähigkeit eines Agenten ab, sinnvolle Informationen über seine Umgebung zu speichern. Dies wird letztlich durch den zugrundeliegenden Kompromiss der Kosteneffizienz gesteuert.

Aufgrund der besprochenen minimalen Implementierung sind alle Bit-Schätzer gleicher Größe gleichwertig. Umwelt-Ensembles einer bestimmten Größe werden ebenfalls als gleichwertig betrachtet. Daher wird die Notation nicht beeinflusst, wenn wir Schätzer und Umgebungen durch ihre Größe identifizieren. Dementsprechend ersetzen wir im Folgenden die Bezeichnungen G und E durch die informativeren Bezeichnungen n bzw. m. Deshalb wird \( \rho^{G}_{E_{m}}(\alpha) \) zu \( \rho^{n}_{m}(\alpha) \), \( p^{-G}_{E} \) wird zu \( p^{-n}_{m} \) etc.

3. Ergebnisse

Die Frage, die dieses Papier motiviert, bezieht sich auf den Kompromiss zwischen schneller Replikation und den Kosten komplexer Inferenzmechanismen. Um diese Frage zu klären, berichten wir über eine Reihe von numerischen Experimenten. Einige dieser Experimente befassen sich mit Schätzern in Umgebungen fester Größe, andere erlauben es den Schätzern, zwischen Umgebungsgrößen zu wechseln, um einen Ort zu finden, an dem sie sich wohlfühlen.

Unser zentrales Ergebnis ist, dass die Komplexität der Schätzer, die eine bestimmte Umgebung bevölkern können, von der Komplexität der Umgebung bestimmt wird (informationstheoretisch ausgedrückt, ergibt sich die Komplexität der am effizientesten replizierten Nachricht aus der Vorhersagbarkeit des Kanals). Um auf die Frage der schnellen Replikation und der Komplexität zurückzukommen: Wir finden Umgebungen, in denen einfache Schätzer aussterben, in denen aber komplexeres Leben gedeiht – und bieten damit ein quantifizierbares Modell für reale Ausflüge in die biologische Komplexität.

Mit unserem Modell können wir nicht nur mathematisch nachweisen, dass die Voraussetzungen für komplexes Leben gegeben sind, sondern auch erforschen und quantifizieren, wann und wie Schätzer zu m-Umgebungen der einen oder anderen Größe gedrängt werden können. Wir beabsichtigen, dieses Modell zu verwenden, um diese Frage in zukünftigen Arbeiten zu untersuchen. Als anschauliche Beispiele berichten wir am Ende dieser Arbeit (i) über die evolutionäre Dynamik, die entsteht, wenn Schätzer gezwungen sind, miteinander zu konkurrieren, und (ii) darüber, wie sich der Kompromiss zwischen schneller Replikation und Komplexität verändert, wenn die Ressourcen erschöpft werden können. Dies sind zwei mögliche evolutionäre Triebkräfte für komplexes Leben, wie unsere numerischen Experimente zeigen.

3.1 Numerische Grenzen der Komplexität von Schätzern

Abbildung 4 zeigt für \( p^{-n}_{m} \) die durchschnittliche Wahrscheinlichkeit, dass n-Schätzer 1 Bit in m-Umgebungen richtig erraten. Der 1-Schätzer (der von maximal dekorrelierten Bits abhängig von der Umgebung lebt) stellt eine untere Grenze dar. Komplexere Maschinen werden im Durchschnitt mehr Bits erraten, außer bei unendlicher Umgebungsgröße \( m \to \infty \), bei der alle Rater die gleiche Vorhersagekraft haben.

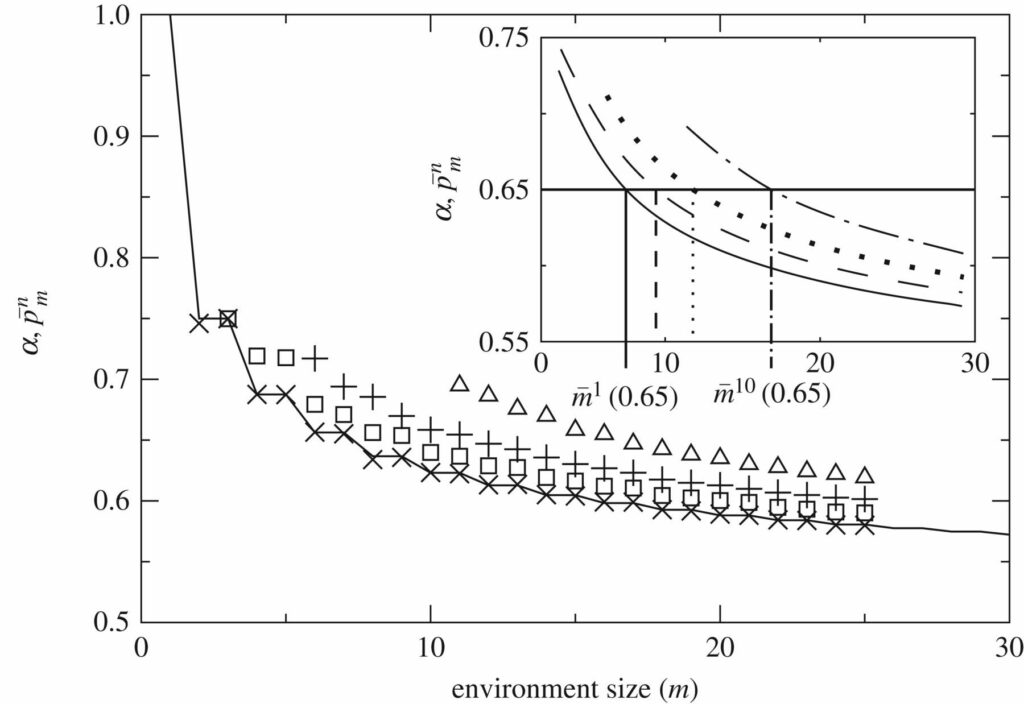
Abbildung 4. Wahrscheinlichkeit des richtigen Erratens eines Bits in Umgebungen konstanter Größe. \( p^{-n}_{m} \): durchschnittliche Wahrscheinlichkeit, dass n-Schätzer 1 Bit in m-Umgebungen für verschiedene n-Werte richtig erraten. Hier kann \( p^{-1}_{m} \) analytisch berechnet werden (durchgezogene Linie im Hauptdiagramm) und markiert eine durchschnittliche untere Grenze der Vorhersagbarkeit für alle Schätzer. In der Abbildung wurden die Daten geglättet und mit einem bestimmten Wert von α verglichen (dargestellt durch eine horizontale Linie). Am Schnittpunkt zwischen dieser Linie und \( p^{-n}_{m} \) finden wir \( m^{-n}(\alpha) \) , die Umgebungsgröße, bei der Agenten der Größe n gerade genug Bits erraten, um bei gegebenem α zu überleben. Beachten Sie, dass n-Schätzer nur in Umgebungen der Größe m≥n ausgewertet werden.

Mit wachsendem m werden die Umgebungen immer weniger vorhersehbar. Wichtig ist, dass die Vorhersagbarkeit kürzerer Wörter schneller abnimmt als die größerer Wörter, so dass Schätzer mit größerem n überleben können, wo andere untergehen würden. Es gibt 2n mögliche n-Wörter, von denen m in jeder m-Umgebung realisiert werden. Wenn m ≫ 2n, implementiert die Umgebung ein effizientes, ergodisches Sampling aller n-Wörter und macht sie damit maximal unvorhersehbar. Wenn \( n \) ≲ \( m < 2^{n} \), ist die Stichprobenziehung von Wörtern der Größe n nicht ergodisch und eine nicht-triviale Struktur in der Umgebung entsteht, weil die Symmetrie zwischen Wörtern der Größe n gebrochen ist – sie können aufgrund von Stichprobeneffekten endlicher Größe nicht gleichmäßig repräsentiert werden.

Dies führt dazu, dass komplexe Schätzer (die in der Lage sind, größere Wörter zu betrachten, sie im Gedächtnis zu behalten und Entscheidungen bezüglich der in größeren Zeichenketten kodierten Informationen zu treffen) im Durchschnitt mehr Bits erraten können als einfachere Agenten. In Bezug auf Nachrichten, die den Kanal überqueren, sind kürzere Wörter bedeutungslos und werden im Grunde nur durch Zufall übertragen (d. h. richtig erraten), während größere Wörter bedeutungsvolle, nicht-triviale Informationen enthalten können, die erfolgreich übertragen werden, weil sie mit der Umgebung auf angemessene Weise zurechtkommen.

Beachten Sie, dass diese Symmetriebrechung zugunsten der Vorhersagbarkeit größerer Wörter nur ein Mechanismus ist, der es uns ermöglicht, Korrelationen auf kontrollierte und messbare Weise einzuführen. In der realen Welt könnte dieser Mechanismus Asymmetrien zwischen dynamischen Systemen in zeitlicher oder räumlicher Hinsicht entsprechen. Obwohl unsere Implementierung eher ad hoc ist (passend zu unseren rechnerischen und konzeptionellen Bedürfnissen), schlagen wir vor, dass ähnliche Mechanismen eine wichtige Rolle bei der Gestaltung des Lebens und der Ausstattung des Universums mit sinnvollen Informationen spielen könnten. In der Tat dürfte es äußerst selten sein, eine Umgebung zu finden, in der Wörter aller Größen gleichzeitig nicht-informativ werden.

Die wechselseitige Information zwischen der Antwort eines Schätzers und der Umgebung (d. h. zwischen den gesendeten Nachrichten und den Kanalbedingungen) ist ein weiteres Merkmal der Vorteile komplexerer Replikatoren. Abbildung 5a zeigt I(G:Em) und 〈I(G:E)〉Em. Wie wir oben festgestellt haben, sind diese Größen nicht identisch. Konzentrieren wir uns für einen Moment auf 1-Schätzer, um zu klären, was diese Größen kodieren.

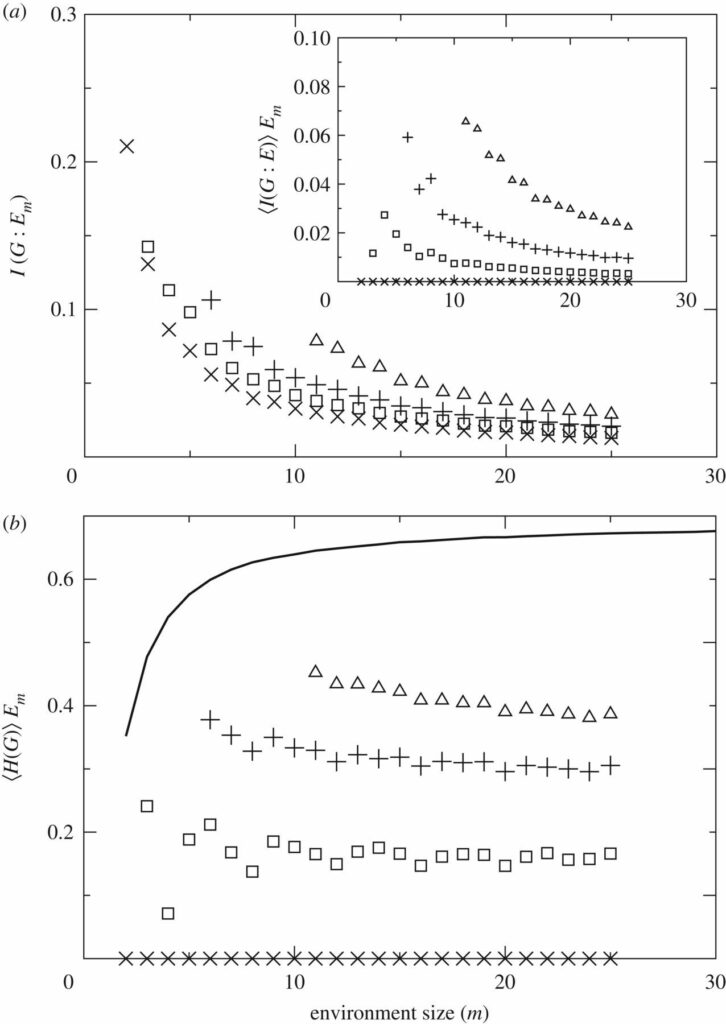
Abbildung 5. Gegenseitige Information und Entropie. Dargestellt sind Schätzer mit n=1 (Kreuze), n=2 (Quadrate), n=5 (Pluszeichen) und n=10 (Dreiecke). (a) I(G:Em) und 〈I(G:E)〉Em (Inset) quantifizieren die verschiedenen Informationsquellen, die es komplexeren Schätzern ermöglichen, in Umgebungen zu gedeihen, in denen einfacheres Leben nicht möglich ist. (b) Die Entropie der Botschaft eines Schätzers in Abhängigkeit von seiner Umgebung scheint in diesen Experimenten trotz der zunehmenden Größe der Umgebung in etwa konstant zu sein. Dies deutet auf ein inhärentes Maß an Komplexität für Schätzer hin. Größere Schätzer sehen zufälliger aus, auch wenn sie möglicherweise mehr aussagekräftige Informationen über ihre Umgebung enthalten. Die dicke schwarze Linie stellt die durchschnittliche Entropie der Umgebungen dar (die sich log(2) nähert), mit der die Entropie der Schätzer verglichen werden kann.

In einer m-Umgebung haben 1-Schätzer nur ein Bit, das sie immer wieder zu senden versuchen. Sie reagieren nicht auf die Umgebung – innerhalb eines Bits ist kein Platz für eine Reaktion, so dass ihre Vermutung immer die gleiche ist. Die gegenseitige Information zwischen dem gesendeten Bit und den beliebigen Wörtern B ⊂ E, auf die die 1-Schätzer stoßen, ist genau Null, wie in Abbildung 5a dargestellt. Daher erfasst 〈I(G:E)〉Em die gegenseitige Information aufgrund der geringen Reaktionsfähigkeit der Schätzer auf die Umweltbedingungen.

Die von den 1-Schätzern ausgesendeten Bits korrelieren zwar nicht mit B ⊂ E, aber sie korrelieren mit jedem gegebenen E, da sie das häufigste Bit in der Umgebung darstellen. Dementsprechend ist die gegenseitige Information zwischen einem 1-Schätzer und den aggregierten Umgebungen (widergespiegelt durch I(G:Em)) von Null verschieden (Hauptfeld von Abbildung 5a). Zu dieser Größe tragen sowohl die Reaktionsfähigkeit der Schätzer als auch die Tatsache bei, dass sie, wie in Abschnitt 2.1 erläutert, mit \( \Gamma^{G}_{E} \) ein nahezu optimales Raten fest verdrahtet haben.

Wir nehmen die Größe eines Schätzers n als grobe Charakterisierung seiner Komplexität. Dies ist gerechtfertigt, weil größere Schätzer komplexere Muster speichern können. 〈H(G)〉Em zeigt, dass komplexere Schätzer entropischer aussehen als weniger komplexe (Abbildung 5b). Größere Schätzer nähern sich dem Entropieniveau der Umgebung an (schwarze dicke Linie in Abbildung 5b), das selbst schnell zu log(2) pro Bit tendiert. Bessere Schätzer erscheinen einem externen Beobachter ungeordneter, auch wenn sie in ihrem Kontext betrachtet bessere Vorhersager sind. Man beachte, dass 〈H(G)〉Em auf der Grundlage der von den Schätzern tatsächlich ausgesandten Bits gebildet wird. In biologischer Hinsicht würde dies bedeuten, dass diese Größe mit der Komplexität des Phänotyps korreliert. Für Schätzer mit fester Größe n beobachten wir einen leichten Abfall von 〈H(G)〉> Em, wenn wir zu größeren Umgebungen übergehen.

Die Schlüsselfrage ist, ob sich komplexere Schätzungssysteme lohnen, wenn sie einen kostspieligeren Mechanismus benötigen, um erfolgreich reproduziert zu werden. Wie bereits erwähnt, könnten wir, wenn wir z. B. ANN oder Bayes’sche Inferenzgraphen zur Modellierung unserer Schätzer verwenden, Kosten für die Anzahl der Einheiten, Knoten oder versteckten Variablen einführen. Diese Fragen sollten vielleicht an anderer Stelle untersucht werden. Hier interessieren wir uns für die mathematische Existenz eines solchen günstigen Kompromisses für ein komplexeres Leben. Um die Diskussion einfach zu halten, entstehen den Bit-Schätzern nur Kosten, die proportional zur Anzahl der Bits sind, die sie zu übertragen versuchen. Es ist zu beachten, dass wir die Allgemeinheit nicht verlieren, da solche Grenzkosten immer existieren werden. Gleichung (2.9) erfasst alle beteiligten Kräfte: die Kosten für die Übermittlung längerer Nachrichten gegenüber der Belohnung für eine erfolgreiche Übertragung.

Schätzer einer bestimmten Größe überleben in einem Umgebungsensemble, wenn sie im Durchschnitt genügend Bits der Umgebung erraten können, oder, um das Bild der Informationstheorie zu verwenden, wenn sie genügend Bits durch den Kanal übertragen können (in jedem Fall überleben sie, wenn \( p^{-n}_{m} > \alpha \), was \( p^{n}_{m} > 0 \) impliziert). Wenn wir einen festen Wert für α festlegen, können wir grafisch die größte Umgebung ermitteln – \( m^{-n}\alpha \) – in der n-Schätzer überleben (Abbildung 4, Einschub). Da m-Umgebungen für komplexere Schätzer vorhersehbarer sind, gilt: \( m^{-n}(\alpha) > m^{-n‘}(\alpha) \), wenn n>n′. Dies garantiert, dass es für α > 0,5 immer m-Umgebungen gibt, aus denen einfaches Leben verbannt wird, während komplexeres Leben gedeihen kann – d. h. Situationen, in denen die Umweltkomplexität ein ausdrücklicher Antrieb für komplexere Lebensformen ist.

Das ist das Ergebnis, das wir angestrebt haben. Mit dem aktuellen Modell können wir mathematisch veranschaulichen, dass es Grenzbedingungen gibt, unter denen komplexere und kostspieligere Inferenzfähigkeiten den Druck zur schnellen und billigeren Replikation überwinden können. Außerdem ermöglicht das Modell eine explizite, informationstheoretisch fundierte Quantifizierung einer solchen Grenze.

3.2 Evolutionäre Triebkräfte

Trotz seiner aufwändigen mathematischen Formulierung halten wir unser Bit-Schätzer-Modell für sehr einfach und vielseitig. Wir glauben, dass es grundlegende informationstheoretische Aspekte biologischer Systeme leicht erfassen kann. In zukünftigen Arbeiten wollen wir es verwenden, um die Beziehungen zwischen Schätzer und Umgebung, innerhalb ökologischer Gemeinschaften oder in einfacheren symbiotischen oder parasitären Situationen zu untersuchen. Um zu veranschaulichen, wie dies funktionieren könnte, stellen wir nun einige minimale Beispiele vor.

Lassen Sie uns zunächst einige Dynamiken untersuchen, bei denen die Schätzer ermutigt werden, komplexere Umgebungen zu erforschen, aber eben diese Komplexität kann zu einer Belastung werden. Wie zuvor bewerten wir einen n-Rater Ng⋅Ne Mal in einer Stichprobe des m-Umgebungsensembles. Betrachten wir auch die akkumulierte Belohnung \( \hat{\rho}^{n}_{m}(\alpha, N_{g}, N_{e}) \) nach diesen Ng⋅Ne-Bewertungen – beachten Sie, dass \( \hat{\rho}^{n}_{m} \) jetzt eine empirische Zufallsvariable ist. Wenn \( \hat{\rho}^{n}_{m}(\alpha, N_{g}, N_{e}) > 0 \), schneidet der n-Schätzer in dieser m-Umgebung gut genug ab und wird ermutigt, eine komplexere Umgebung zu erkunden. Infolgedessen wird der Schätzer in eine (m+1)-Umgebung befördert, wo er erneut bewertet wird. Wenn \( \hat{\rho}^{n}_{m}(\alpha, N_{g}, N_{e}) < 0\), stellt diese m-Umgebung für den n-Schätzer eine zu große Herausforderung dar, und er wird in eine (m-1)-Umgebung zurückgestuft. Man beachte, dass der n-Schätzer selbst immer eine feste Größe hat. Es ist die Komplexität der Umgebung, die sich in Abhängigkeit von der angesammelten Belohnung ändert.

Bei der wiederholten Auswertung des n-Schätzers entsteht eine gewisse Dynamik, die den Schätzer mehr oder weniger komplexe Umgebungen erkunden lässt. Der stationäre Zustand dieser Dynamik wird durch eine Verteilung Pn(m,α) charakterisiert. Diese gibt die Häufigkeit an, mit der n-Schätzer in Umgebungen einer bestimmten Größe gefunden werden (Abbildung 6a). Jeder n-Schätzer hat seine eigene Verteilung, die die Komplexität der Umgebung wiedergibt, mit der der Schätzer am besten zurechtkommt. Die Überschneidungen und Lücken zwischen Pn(m,α) für verschiedene n deuten darauf hin, dass: (i) einige Schätzer in einen harten Wettbewerb treten würden, wenn sie sich Umgebungen einer bestimmten Art teilen müssten, und (ii) es Raum für verschiedene Schätzer gibt, sich in Umgebungen mit zunehmender Komplexität aufzuteilen.

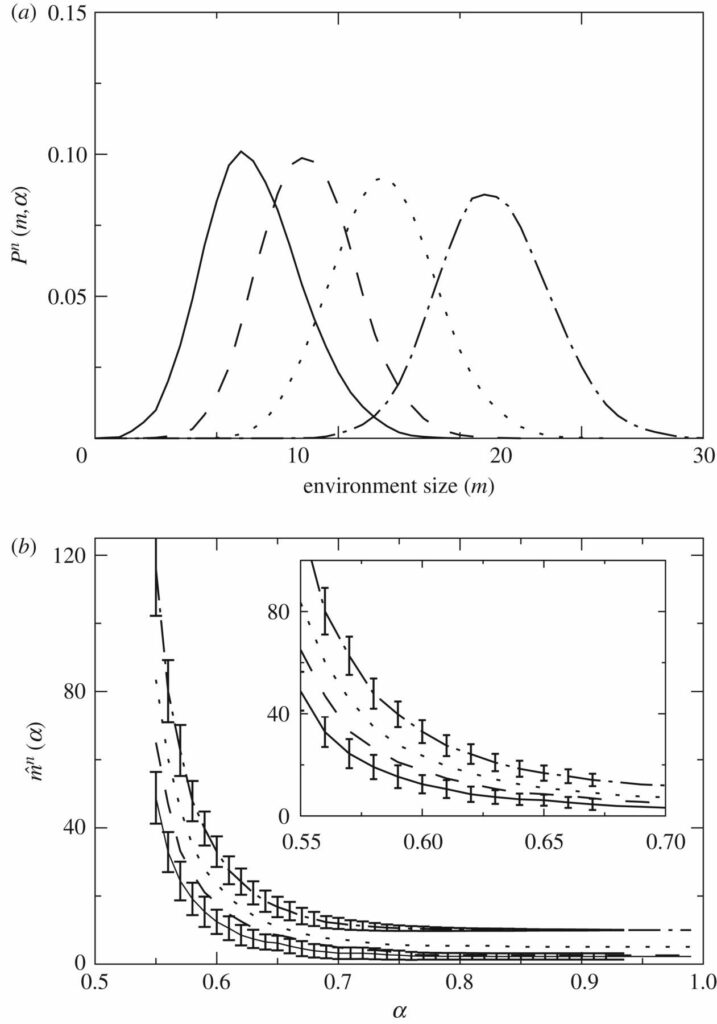
Abbildung 6. Dynamik in der Umgebung \( m^{-n}(\alpha)\). Wiederum Schätzer mit n=1 (durchgezogene Linie), n=2 (gestrichelte Linie), n=5 (gepunktete Linie) und n=10 (punktgestrichelte Linie). (a) Pn(m,α) gibt an, wie oft wir n-Schätzer in m-Umgebungen finden, wenn sie sich nur aufgrund ihrer Überlebensfunktion \( \rho^{n}_{m} \) frei bewegen dürfen. Der zentrale Wert \( \hat{m}^{n} \) von Pn(m,α) muss auf \( m^{-n}(\alpha) \) konvergieren, und die Oszillationen um ihn herum hängen (durch Ng und Ne) davon ab, wie oft wir die Schätzer in jeder Umgebung bewerten. (b) \( \hat{m}^{n} \)-Mittelwert für n=1,2,5,10 und Standardabweichung von Pn(m,α) für n=1,10. Die Abweichungen werden für n=2,5 aus Gründen der Übersichtlichkeit nicht dargestellt. Der Inset stellt eine Vergrößerung der Hauptdarstellung dar.

Der Durchschnitt

\( \hat{m}^{n}(\alpha) = \sum_{m}mP^{n}(m, \alpha) \qquad \enspace \enspace \enspace \enspace \enspace \enspace \) 3.1

sollte unter dem entsprechenden Grenzwert auf \( \hat{m}^{n}(\alpha) \) ≃ \( \bar{m}^{n}(\alpha) \) konvergieren. Das heißt, wenn wir die Schätzer oft genug numerisch auswerten, sollte der empirische Wert \( \hat{m}^{n}(\alpha) \) gegen den in Abbildung 4 gezeigten Mittelwert des Feldes, \( \bar{m}^{n}(\alpha) \), konvergieren. Abbildung 6b zeigt die dynamisch abgeleiteten Mittelwerte \( \hat{m}^{n}(\alpha) \) und einige Abweichungen um sie herum als Funktion von α.

Es ist leicht zu rechtfertigen, dass sich Schätzer in einfachere Umgebungen zurückziehen, wenn sie mit einer großen Komplexität nicht zurechtkommen. Es ist weniger klar, warum sie kompliziertere Umgebungen suchen sollten, wenn sie in einer gegebenen Umgebung gut zurechtkommen. Dies könnte der Fall sein, wenn eine äußere Kraft sie dazu treibt; zum Beispiel, wenn einfachere Schätzer (die in einfacheren Umgebungen effizienter sein könnten) den Ort bereits überfüllt haben. Erinnern wir uns anhand von Abbildung 4 daran, dass bei einer bestimmten Umgebungsgröße komplexere Schätzer immer eine größere Belohnung anhäufen können. Dies könnte darauf hindeuten, dass sich komplexe Schätzer immer lohnen, aber die zusätzliche Komplexität könnte energetisch gesehen zu einer Belastung werden – man denke z. B. an die übertriebenen metabolischen Kosten von Säugetiergehirnen. Es ist nicht trivial, wie sich die Wettbewerbsdynamik zwischen unterschiedlich großen Schätzern abspielen kann. Lassen Sie uns anhand eines einfachen Modells einige Erkenntnisse gewinnen.

n-Schätzer mit n=0, 1, 2, 3 und 4 wurden nach dem Zufallsprinzip verteilt und besetzten 100 Umgebungen, alle mit der festen Größe m. Diesen Schätzern wurde ein Initial \( \hat{\rho}_{i}(t = 0) = n_{\rho0} \) zugewiesen. Dabei bezeichnet i=1,…,100 jeden der 100 verfügbaren Schätzer. Größere Schätzer beginnen mit einem größeren Ausgangswert, was bedeutet, dass sie mit einer größeren metabolischen Last zufrieden sind. Ein 0-Schätzer steht für eine unbesetzte Umgebung. Neue leere Umgebungen können nur entstehen, wenn tatsächlich (n≠0) Schätzer sterben, wie wir weiter unten erklären. Wir verfolgten die Population mit Pm(n,t), dem Anteil der 0-, 1-, 2-, 3- und 4-Schätzer über die Zeit.4

Bei jeder Iteration wurde ein Schätzer (z.B. der i-te) zufällig ausgewählt und in Bezug auf seine Umgebung bewertet. Dann wurde die verbrauchte Umgebung durch eine neue, zufällige Umgebung mit der gleichen Größe ersetzt. Wir haben sichergestellt, dass jeder Schätzer im Durchschnitt die gleiche Anzahl von Bits zu erraten versucht. Das bedeutet z.B., dass 1-Schätzer doppelt so oft getestet werden wie 2-Schätzer, usw. Wenn nach der Auswertung festgestellt wurde, dass \( \hat{\rho}_{i}(t + \Delta t) < 0 \), hat der Schätzer nicht mehr funktioniert und wurde durch einen neuen ersetzt. Das n des neuen Schätzers wurde zufällig nach der aktuellen Verteilung Pm(n,t) gewählt. Wenn \( \hat{\rho}_{i}(t + \Delta t) > 2n\rho_{0} \), dann wurde der Schätzer repliziert und teilte sein \( \hat{\rho}_{i} \) mit seiner Tochter, die einen anderen zufällig gewählten Schätzer überholte. Diese Replikation bei 2nρ0 bedeutet, dass die Eltern vor der Erzeugung eines ähnlichen Agenten eine metabolische Belastung erfüllen müssen, die mit ihrer Größe wächst. Es gibt einen Bereich (\( 0 < \hat{\rho}_{i} < 2n\rho_{0} \)), in dem die Schätzer lebendig sind, sich aber nicht vermehren.

Natürlich ist dieses Minimalmodell nur ein Proxy, und es könnten weichere Bedingungen gestellt werden. Diese könnten z. B. eine zufällige Replikation in Abhängigkeit vom akkumulierten \( \hat{\rho}_{i}(t + \Delta t) \) zulassen, oder eine größere Nachkommenschaft, wenn \( \hat{\rho}_{i}(t + \Delta t) \gg 2n\rho_{0} \). Dies sind interessante Varianten, die es wert sein könnten, erforscht zu werden. Auch aus dem hier betrachteten einfachen Aufbau lassen sich einige Erkenntnisse gewinnen. Wir gehen davon aus, dass komplexere Modelle die folgenden Sondierungsergebnisse weitgehend übernehmen werden.

Abbildung 7a,b zeigt Pm(n,t=10 000) mit α=0,6 und 0,65. Man beachte, dass bei großen Umgebungen alle Schätzer zusammen nicht 100 ergeben. Sie liegen sogar unter dieser Zahl, d. h. es bleiben meist leere Felder übrig. Der am häufigsten vorkommende Schätzer nach 10.000 Iterationen ist in Abbildung 7c als Funktion von m und α dargestellt.

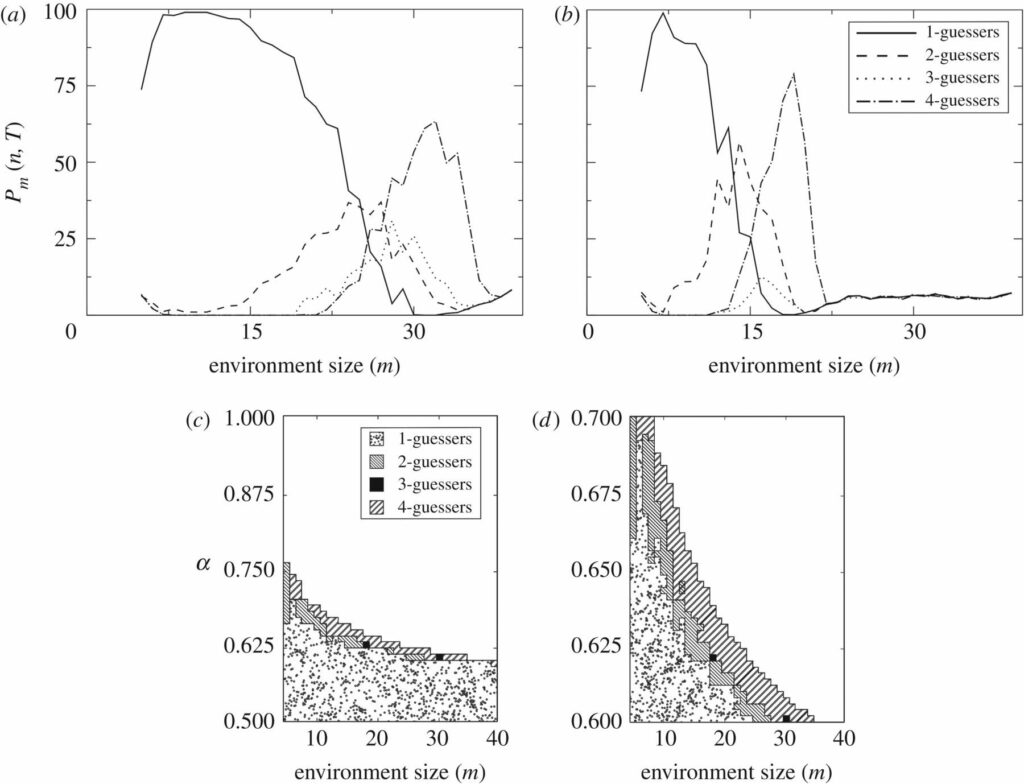
Abbildung 7. Evolutionäre Triebkräfte: Wettbewerb. Koexistierende Replikatoren werden die Umgebungen der anderen auf nicht-triviale Weise beeinflussen, was oft zu Wettbewerb führen kann. Wir implementieren eine Dynamik, bei der 1-, 2-, 3- und 4-Schätzer ausschließlich eine endliche Anzahl von Umgebungen einer bestimmten Größe (festes m) besetzen. Die 100 verfügbaren Slots werden bei t=0 zufällig besetzt und im weiteren Verlauf der Dynamik an die besten Replikatoren vergeben. Wir zeigen Pm(n,t=10.000) für m=5,…,39 und α=0.6 (a) und α= 0.65 (b). Der häufigste Schätzer bei t=10.000 ist für α ∈ (0.5,1) (c) und α ∈ (0.6,0.7) (d) dargestellt. Sobald m festgelegt ist, gibt es einen oberen Wert von α, oberhalb dessen kein Schätzer überlebt und alle 100 verfügbaren Slots leer bleiben. Durch den Wettbewerb und den Kompromiss zwischen Replikation und Vorhersagbarkeit werden die Schätzer entsprechend der Komplexität der Umgebung, d. h. des Übertragungskanals, getrennt. Die Koexistenz verschiedener Schätzer scheint möglich zu sein (z. B. m=15 in b), aber es kann nicht garantiert werden, dass die Dynamik zu einer stetigen Verteilung konvergiert.

Diese Diagramme zeigen, wie sich die Schätzer in Abhängigkeit von ihrer Komplexität auf natürliche Weise in Umgebungen aufteilen, wobei einfachere Schätzer, wie oben vorgeschlagen, einfachere Umgebungen bevölkern. In solch einfachen Umgebungen reicht die zusätzliche Belohnung, die komplexere Schätzer erhalten, nicht aus, um ihre energetischen Kosten auszugleichen, und sie verlieren in diesem direkten Wettbewerb. Sie werden daher in komplexere Umgebungen gedrängt, wo sich ihre kostspielige Inferenzmaschinerie auszahlt.

Nach 10.000 Iterationen beobachten wir auch Fälle, in denen verschiedene Schätzer nebeneinander existieren. Das bedeutet, dass die mathematischen Grenzen, die dieses naive Modell setzt, keine unmittelbare, absolute Dominanz des am besten angepassten Schätzers implizieren. Interessante zeitliche Dynamiken können entstehen und bieten die Möglichkeit, komplexe ökologische Interaktionen zu modellieren.

Bisher haben unsere Schätzer nur passiv mit der Umwelt interagiert, indem sie die Belohnung erhielten, die die entsprechende m-Umgebung vorgibt. Aber lebende Systeme gestalten im Gegenzug auch ihre Nische. Ein solches Zusammenspiel kann sehr kompliziert werden, und wir glauben, dass unser Modell ein leistungsfähiges Forschungsinstrument darstellt. Lassen Sie uns einen sehr einfachen Fall untersuchen, in dem die Handlungen der Schätzer (d. h. ob sie etwas richtig erraten oder nicht) die Belohnung beeinflussen, die eine Umgebung bieten kann.

Dazu stellen wir uns die Bits in einer Umgebung als Ressourcen vor, die nicht nur erschöpft werden können, wenn sie richtig erraten wurden, sondern auch wieder aufgefüllt werden können, wenn genügend Zeit verstrichen ist. Aus der Perspektive der Nachrichtenübermittlung könnte eine Stelle auf dem Kanal auch überfüllt erscheinen, wenn sie gerade eine erfolgreiche Übertragung durchführt. Nehmen wir an, dass jedes Mal, wenn ein Bit richtig erraten wird, es mit einer Effizienz β erschöpft (oder überfüllt) wird, so dass im Durchschnitt jedes Bit keine Belohnung \( \beta(p^{-n}_{m}/m) \) der Zeit beitragen kann. Die durchschnittliche Belohnung, die ein Schätzer aus einem Ensemble zieht, beträgt

\( \tilde{r}^{n}_{m} = (1 – \beta \frac{\bar{p}^{n}_{m}}{m})\bar{p}^{n}_{m}r \)

die in Abbildung 8 für 1-, 2-, 5- und 10-Ratgeber und β=1 aufgetragen ist.

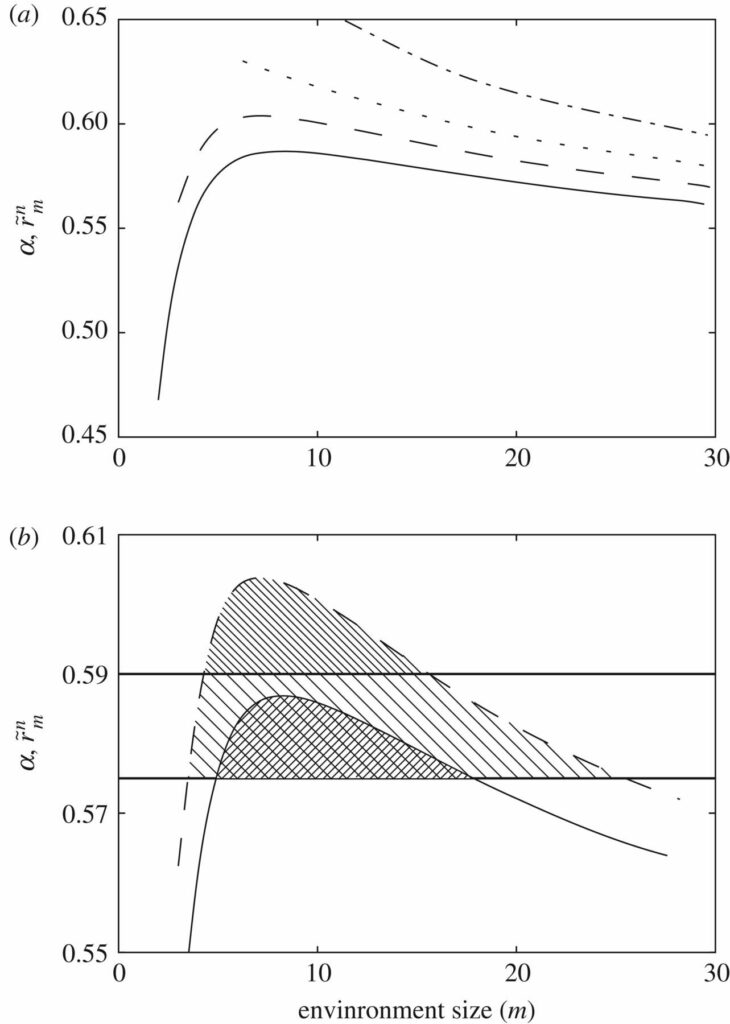
Abbildung 8. Evolutionäre Treiber: erschöpfte Ressourcen. Anstatt Kanalschlitze zu monopolisieren (wie in Abbildung 5), können wir uns einzelne Bits auch als wertvolle, endliche Ressourcen vorstellen, die erschöpft werden, sobald sie richtig erraten werden. Dann kann ein erfolgreicher Replikator seine eigene Umgebung verderben, und es können neue Bedingungen gelten, unter denen Leben möglich ist. (a) Durchschnittliche Belohnung von 1-, 2-, 5- und 10-Schätzern in Umgebungen unterschiedlicher Größe, wenn die Bits mit einer Effizienz von β=1 erschöpft werden, sobald sie richtig erraten wurden. (b) Bei α=0,575 und α=0,59 können 1- und 2-Schätzer innerhalb der oberen und unteren Umgebungsgrößen überleben. Wenn die Umgebung zu klein ist, werden die Ressourcen schnell verbraucht und die Replikatoren können nicht überleben. In der Sprache der Nachrichtenübermittlung überfüllen die Schätzer ihren eigenen Kanal. Wenn die Umgebung zu groß ist, übernimmt die Unberechenbarkeit die Oberhand über diese einfachen Replikatoren und sie gehen unter.

Kleinere Schätzer, die in sehr kleinen Umgebungen leben, überfüllen schnell ihre Kanäle (oder erschöpfen die Ressourcen, von denen sie abhängen). In Abbildung 8b (immer noch mit β=1) können 1- und 2-Schätzer bei einem bestimmten α nur innerhalb bestimmter unterer und oberer Grenzen überleben. Auch die Steigung der Kurven um diese Grenzen herum gibt uns wichtige Informationen. Wenn sich diese Schätzer in Umgebungen um die untere Grenze herum aufhalten (d. h. in der Nähe der kleinsten m-Umgebung, in der sie überleben können), dann werden sie bei einem Umzug in größere Umgebungen immer größere Belohnungen erhalten. Wenn sie sich jedoch in der Nähe der Obergrenze aufhalten, ist ein Wechsel in größere Umgebungen immer nachteilig. Mit anderen Worten: Dynamiken wie die zu Beginn dieses Abschnitts vorgestellte (siehe Abbildung 6a) hätten instabile bzw. stabile Fixpunkte an der oberen bzw. unteren Grenze des Fortbestands.

Dieses einfache Modell veranschaulicht, wie Ressourcenknappheit (und, allgemeiner, andere Arten von Wechselwirkungen zwischen Schätzer und Umwelt) eine wichtige Rolle als evolutionäre Triebkraft für komplexeres Leben spielen könnten. Es handelt sich hierbei weder um ein erschöpfendes noch um ein endgültiges Modell, sondern lediglich um eine Veranschaulichung der Vielseitigkeit der in dieser Arbeit vorgestellten Bit-Schätzer und Umgebungen.

4. Diskussion

In diesem Papier haben wir uns mit einer grundlegenden Frage im Zusammenhang mit der Entstehung von Komplexität in lebenden Systemen beschäftigt. Dabei geht es um die Frage, ob die mathematischen Voraussetzungen dafür gegeben sind, dass komplexere Organismen die Kosten ihrer Komplexität überwinden können, indem sie ein höheres Potenzial zur Vorhersage der äußeren Umgebung entwickeln. Wie von mehreren Autoren vorgeschlagen [6-8], kann die Verhaltensplastizität, die durch das Erkundungsverhalten lebender Systeme entsteht, im Hinblick auf ihre Fähigkeit, mit Umweltinformationen umzugehen, verstanden werden [59].

Unsere Modelle verfolgen einen expliziten Ansatz, indem sie unter sehr allgemeinen Annahmen einen Kompromiss zwischen Replikation und Vorhersagbarkeit in Betracht ziehen, nämlich: (i) komplexere Umgebungen erscheinen einfacheren Replikatoren unvorhersehbarer und (ii) Agenten, die ein größeres Gedächtnis haben und Schlussfolgerungen auf der Grundlage besser ausgearbeiteter Informationen ziehen können, können genügend wertvolle Bits aus der Umwelt extrahieren, um in diesen schwierigeren Situationen zu überleben. Trotz der unvermeidlichen Kosten, die der kognitiven Maschinerie inhärent sind, wird gezeigt, dass es einen Selektionsprozess hin zu komplexerem Leben gibt. Dies ebnet den Weg für einen eindeutigen evolutionären Druck in Richtung komplexerer Lebensformen.

In unserer Studie identifizieren wir einen Sender (Replikatoren in einer bestimmten Generation), einen Empfänger (Replikatoren in der nächsten Generation) und einen Kanal (beliebige Umweltbedingungen), über den eine Botschaft (idealerweise Anweisungen, wie man neuere Replikatoren baut) weitergegeben wird. Die darwinistische Evolution folgt auf natürliche Weise, da effektive Replikatoren einen Kanal schneller und zuverlässiger durchqueren und so in den nachfolgenden Generationen immer mehr Platz erhalten. Die Inferenzaufgabe ist implizit, da die Umwelt selbst sinnvolle Informationen kodiert, die, wenn sie von den Replikatoren aufgenommen werden, die Fitness der Phänotypen, die durch die erfolgreichen Nachrichten verkörpert werden, erhöhen.

Diese Sichtweise lehnt sich direkt an ein früheres qualitatives Bild an, das von Maynard-Smith [18] eingeführt wurde. In dieser Metapher wurde der DNA eine externe Bedeutung zugewiesen, die gegenüber dem Umgebungsrauschen bewahrt werden musste. Im Gegensatz dazu schlagen wir vor, dass bei dem Versuch, Nachrichten von einer Generation zur nächsten zu übertragen, alle Kanalbedingungen (einschließlich Rauschen) relevante Bits in die übertragenen Strings pumpen – daher besteht keine Notwendigkeit, die Bedeutung vor dem Kanal zu schützen, da bedeutungsvolle Informationen tatsächlich aus der Interaktion des Replikators mit solchen Kanalkontingenzen hervorgehen.

Die Art und Weise, wie wir in unserem Schema Korrelationen einführen (durch einen Symmetriebruch zwischen der Information, die von kurzen und größeren Wörtern getragen wird, aufgrund von Endlichkeitseffekten), ist mit dieser Sichtweise vereinbar. Interessanterweise deutet dies aber auch darauf hin, dass sinnvolle Informationen auch in stark unstrukturierten Umgebungen auf natürliche Weise entstehen können, wenn unterschiedliche räumliche und zeitliche Maßstäbe eine wichtige Rolle spielen. Unsere Ergebnisse deuten darauf hin, dass die Komplexität der Umwelt eine Triebkraft für die Komplexität des Lebens ist, aber es bleibt die Frage: „Woher kommt all diese Umweltkomplexität überhaupt?“ Die Art und Weise, wie wir Komplexität und Umweltgröße miteinander verknüpfen, legt eine Antwort nahe: dass lebende Systeme die Möglichkeit haben, sich in immer größeren Umgebungen zu bewegen (die aufgrund ihrer schieren Größe komplexer sind als kleinere). Dies entspricht in etwa den in Abbildung 6 dargestellten Simulationen. Eine andere Möglichkeit ist, dass lebende Systeme selbst ihre Umwelt verändern.

Diese Art der Integration von Informationstheorie und darwinistischer Evolution eignet sich für die Analyse der vorliegenden Fragen, die die Entstehung komplexer Lebensformen betreffen. Aber sie legt auch weitere Forschungslinien nahe. Wie zu Beginn des Papiers erörtert, können und sollten Schätzer und ihre übertragbaren Botschaften den Übertragungskanal formen (z. B. durch Verdrängung, wie in Abschnitt 3.2 kurz erörtert). Welche möglichen co-evolutionären Dynamiken zwischen Schätzer und Kanal können festgestellt werden? Gibt es stabile Dynamiken, andere, die zum Aussterben führen, usw.? Bedeuten einige von ihnen vielleicht eine unbefristete Evolution? Aber welche? Diese Fragen stehen in engem Zusammenhang mit dem Phänomen der Nischenbildung und hängen mit der im vorigen Absatz gestellten Frage nach den vielen möglichen Ursprüngen der Umweltkomplexität zusammen. Wir schlagen vor, dass sie sich leicht mit dem Bit-Schätzer-Paradigma modellieren lassen, das wir in dieser Arbeit vorgestellt haben. Um die Vielseitigkeit des Modells weiter zu erforschen, könnte die von einem Schätzer übermittelte Nachricht als Umwelt an sich betrachtet werden, was die Tür zur Modellierung von Ökosystemen auf der Grundlage der reinen Informationstheorie öffnet. Dies regt auch dazu an, verschiedene symbiotische Beziehungen aus dieser Perspektive zu erforschen und zu untersuchen, wie sie sich auf die Coevolution auswirken könnten.

Eine wichtige Frage, die den Kompromiss zwischen Speicher und Anpassungsfähigkeit von Bit-Schätzern betrifft, wurde beiseite gelassen. Hier haben wir Schätzer mit einer minimalen Anpassungsfähigkeit untersucht, um uns auf die entstehende Hierarchie der Komplexität zu konzentrieren. Anpassungsfähigkeit auf schnelleren (z. B. verhaltensbezogenen) Zeitskalen ist mit komplexeren Schlussfolgerungen mit größerer Dynamik verbunden. Dies bringt neue Dilemmata mit sich, wie die verschiedenen Bausteine komplexer Schlussfolgerungen zu gewichten sind – wie vergleichen wir z. B. Speicher und If-Else- oder While-Anweisungen? Diese und andere Fragen müssen in der zukünftigen Forschung untersucht werden.

Abschließend ist es interessant, unsere Ergebnisse in einen Zusammenhang mit zwei neueren Arbeiten zu stellen, die nach Abschluss dieser Arbeit veröffentlicht wurden. Einerseits erörtern Boyd et al. [60], wie sich ein System wie ein thermodynamischer Motor verhalten kann, der mit Umweltkorrelationen als Treibstoff Arbeit produziert. Dies ist unserer Meinung nach eine sehr relevante Diskussion über die thermodynamischen Grenzen biophysikalischer Systeme, die unseren abstrakten Kosten und Belohnungen eine explizite Bedeutung verleihen könnte. Andererseits untersuchen Marzen & DeDeo [34] die Beziehung zwischen einer Umgebung und den Ressourcen, die für die Sinneswahrnehmung eingesetzt werden. Sie verwenden einen utilitaristischen Ansatz, um zwei Regime zu entdecken: eines, in dem die Kosten der Sinneswahrnehmung mit der Komplexität der Umgebung wachsen, und ein anderes, in dem diese Kosten weitgehend unabhängig von der Komplexität der Umgebung bleiben. Die Autoren sagen also, dass die verlustbehaftete Kompression es lebenden Systemen ermöglicht, zu überleben, ohne alle Informationen in der Umwelt erschöpfend zu erfassen. In diesen beiden Arbeiten werden die Replikation und der Druck der darwinistischen Selektion nicht so explizit erörtert wie in unserer Forschung, aber beide Arbeiten bringen interessante Elemente ein, die den Bit-Schätzer-Rahmen bereichern können.

Zugänglichkeit der Daten

Dieses theoretische Papier stützt sich nicht auf empirische Daten. Alle Diagramme können anhand der Gleichungen und Anweisungen in diesem Papier erstellt werden.

Beiträge der Autoren

Beide Autoren haben gleichermaßen zu dieser Arbeit beigetragen. Sowohl L.F.S. als auch R.V.S. entwarfen und implementierten den theoretischen Rahmen, analysierten die Daten, erstellten die Abbildungen und schrieben das Manuskript. Beide Autoren haben die endgültige Fassung dieses Manuskripts gelesen und genehmigt.

Interessenskonflikte

Wir erklären, dass wir keine Interessenskonflikte haben.

Finanzierung

Diese Forschungsarbeit wurde von der Botin-Stiftung, von der Banco Santander über ihre Santander Universities Global Division, vom Santa Fe Institute, vom Secretaria d’Universitats i Recerca del Departament d’Economia i Coneixement de la Generalitat de Catalunya und vom Europäischen Forschungsrat mit dem ERC-Grant Nr. ERC SYNCOM 294294 unterstützt.

Danksagungen

Die Autoren danken den Mitgliedern des Complex Systems Lab sowie Jeremy Owen, Henry Lin, Jordan Horowitz und David Wolpert für sehr nützliche Diskussionen.

Fußnoten

1 Man beachte, dass viele der phänotypischen Strukturen, die aufgebaut werden, um sich zu vermehren, später wieder verworfen werden (man denke z. B. an die Keim- und somatischen Zelllinien). Zur Veranschaulichung haben wir eine klare Trennung zwischen Genotyp und Phänotyp vorgenommen. Wir sind uns bewusst, dass die Grenze zwischen diesen Begriffen fließend ist.

2 Es gibt einen untersuchenswerten Kompromiss zwischen der Wiedergabetreue der Botschaft, die ein Agent zu vermitteln versucht, und seiner Fähigkeit, auf Umweltbedingungen in Echtzeit zu reagieren. Die Erforschung dieses Kompromisses ist ein Thema für zukünftige Arbeiten. Bis dahin werden die Reaktionsfähigkeiten unserer Bit-Schätzer auf ein Minimum beschränkt bleiben.

3 Es sei darauf hingewiesen, dass komplexere Schätzer nicht nur ihre Vermutung zurücksetzen würden. Sie könnten auch einen Baum mit bedingten Anweisungen an jedem Punkt durchsuchen. Neben einem erweiterten Speicher für die wachsende Zahl von Verzweigungen würden sie auch verschachtelte If-Else-Anweisungen benötigen. Andererseits könnten ANNs oder Bayes’sche Netze ein solches Durchsuchen von Bäumen ohne übermäßige If-Else-Kosten realisieren.

4 Diese Experimente waren rechenaufwändiger, weshalb wir n=1,2,3,4 anstelle der in der gesamten Arbeit verwendeten Werte n=1,2,5,10 verwendet haben. Die aus den Simulationen gewonnenen Erkenntnisse hängen nicht von den tatsächlichen Werten von n ab.

Verweise

Tags: , , ,

More Stories

Das Bewusstsein: Hier, dort und überall? – Giulio Tononi, Christof Koch

Axel Krauss April 13, 2024 0

Schreibe einen Kommentar