Retrokausalität in der Quantenmechanik – Simon Friederich, Peter W. Evans

Quelle: Retrocausality in Quantum Mechanics (Stanford Encyclopedia of Philosophy)

Die Quantentheorie bietet einen Rahmen für die moderne theoretische Physik, der sich durch enorme Vorhersage- und Erklärungskraft auszeichnet. Angesichts des sogenannten „Messproblems“ besteht jedoch kein Konsens darüber, wie die physische Realität beschaffen sein könnte, damit dieser Rahmen diesen Erfolg hat. Die Theorie ist somit ein äußerst gut funktionierender Algorithmus zur Vorhersage und Erklärung der Ergebnisse von Beobachtungen, aber es besteht kein Konsens darüber, welche Art von objektiver Realität diesen Beobachtungen plausibel zugrunde liegen könnte.

Unter den vielen Versuchen, eine „Interpretation“ der Quantentheorie zu liefern, um diesen Vorhersage- und Erklärungserfolg zu erklären, geht eine Klasse von Interpretationen von rückwärts in der Zeit laufenden kausalen Einflüssen – Retrokausalität – als Grundlage für die Erstellung einer überzeugenden grundlegenden Darstellung der Quantentheorie aus. Dieser Beitrag gibt einen Überblick über retrokausale Ansätze zur Interpretation der Quantentheorie, die Hauptgründe für die Annahme dieses Ansatzes, eine Auswahl konkreter vorgeschlagener retrokausaler Modelle und eine Übersicht über die Einwände, die gegen solche Ansätze vorgebracht werden.

1. Geschichte

Von der Geburt der Theorie der Quantenmechanik im Jahr 1925/6 bis zum Ausbruch des Krieges in Europa bildete sich eine klare Orthodoxie im konzeptionellen und ontologischen Rahmen für das Verständnis der Quantentheorie heraus. Dieser Rahmen, der heute als Kopenhagener Deutung bekannt ist, verkörperte die positivistischen Tendenzen von Heisenberg und Bohr und stand im Gegensatz zu den eher realistischen Tendenzen von de Broglie, Einstein und Schrödinger. Erst mit dem Bellschen Theorem in den 1960er Jahren und seinen experimentellen Tests in den 1970er und 1980er Jahren wurde dieser Interpretationsdebatte neue Energie eingehaucht. Allerdings gab es bereits ab Mitte der 1940er Jahre erste Vorschläge zur Retrokausalität als Teil des konzeptionellen und ontologischen Rahmens in der Quantentheorie.

Es gibt zwei Schlüsselideen, die die historische Entwicklung des Konzepts der Retrokausalität in der Quantenmechanik prägen. Der erste Vorschlag eines rückwirkenden Einflusses in der Quantenmechanik stammt von Wheeler und Feynman (1945, 1949). Sie kamen auf diese Idee, als sie über die potenziell klassischen Ursprünge einiger Schwierigkeiten der Quantentheorie nachdachten. Betrachten wir das folgende Problem aus der klassischen Elektrodynamik: Ein beschleunigtes Elektron sendet elektromagnetische Strahlung aus und durch diesen Prozess wird die Beschleunigung des Elektrons gedämpft. Verschiedene Versuche, dieses Phänomen im Rahmen der klassischen Theorie der Elektrodynamik zu erklären, waren entweder empirisch unzureichend oder ließen eine kohärente physikalische Interpretation vermissen. Wheeler und Feynman versuchten, diese Situation durch eine Neuinterpretation von Diracs (1938) Theorie der strahlenden Elektronen zu beheben.

Der Kern von Wheelers und Feynmans vorgeschlagener „Absorber-Theorie der Strahlung“ ist der Vorschlag, dass der Prozess der Emission und Absorption elektromagnetischer Strahlung als eine Wechselwirkung zwischen einer Quelle und einem Absorber und nicht als ein unabhängiger elementarer Prozess betrachtet werden sollte (diese Idee geht auf Tetrode (1922) und G. Lewis (1926) zurück.) Wheeler und Feynman stellen sich eine beschleunigte Punktladung in einem absorbierenden System vor und betrachten die Art des mit der Beschleunigung verbundenen elektromagnetischen Feldes. Man kann sich vorstellen, dass eine elektromagnetische Störung „zunächst“ von der Quelle nach außen wandert, um jedes Teilchen des Absorbers zu stören. Die Teilchen des Absorbers erzeugen dann gemeinsam ein nachfolgendes Feld. Nach der Wheeler-Feynman-Theorie besteht dieses neue Feld aus der Hälfte der Summe der verzögerten (vorwärts in der Zeit) und vorgezogenen (rückwärts in der Zeit) Lösungen der Maxwell-Gleichungen. Die Summe der vorgezogenen Effekte aller Teilchen des Absorbers ergibt dann ein vorgezogenes ankommendes Feld, das gleichzeitig mit dem Zeitpunkt der Emission an der Quelle vorhanden ist (siehe jedoch Abschnitt 5 für weitere Informationen darüber, wie man diesen „Prozess“ verstehen sollte). Die Behauptung ist, dass dieses fortgeschrittene Feld eine endliche Kraft auf die Quelle ausübt, die genau die erforderliche Größe und Richtung hat, um die beobachtete Energieübertragung von der Quelle zum Absorber zu erklären; dies ist Diracs Strahlungsdämpfungsfeld. Wenn dieses fortgeschrittene Feld mit dem äquivalenten halb verzögerten, halb fortgeschrittenen Feld der Quelle kombiniert wird, ist die beobachtete Gesamtstörung das vollständig verzögerte Feld, von dem empirisch bekannt ist, dass es von beschleunigten Punktladungen emittiert wird.

Der entscheidende Punkt, der beim Wheeler-Feynman-Schema beachtet werden muss, ist, dass aufgrund des vorauseilenden Feldes des Absorbers das Strahlungsdämpfungsfeld genau zum Zeitpunkt der anfänglichen Beschleunigung an der Quelle vorhanden ist. Dieses Schema von vorauseilenden und nacheilenden Wellen bildet nun die Grundlage für das vollständigste retrokausale Modell der Quantenmechanik, die Transaktionsinterpretation (siehe §5).

Die zweite Schlüsselidee in der historischen Entwicklung der Retrokausalität in der Quantenmechanik taucht etwa zur gleichen Zeit auf wie die Absorbertheorie von Wheeler und Feynman. Der französische Physiker Costa de Beauregard, ein Schüler von de Broglie, bemerkte einen potenziellen Einwand gegen die Argumentation in Einsteins, Podolskys und Rosens berühmter Arbeit (1935) über die Vollständigkeit der Quantenmechanik (siehe den Eintrag über das Einstein-Podolsky-Rosen-Argument in der Quantentheorie), das heute allgemein als EPR-Argument bekannt ist. Einstein et al. argumentieren, dass die Quantenmechanik auf der Grundlage der folgenden Annahme unvollständig sein muss: Es ist nicht zu erwarten, dass eine vernünftige Definition der Realität zulässt, dass die Realität eines Systems von dem Messprozess abhängt, der an einem anderen entfernten System durchgeführt wird, das das erste System in keiner Weise stört. Die wichtigste Bedingung, die Einstein et al. für jede vernünftige Definition der Realität vorschlagen, ist, dass „es keine Interaktion mehr zwischen den beiden Teilen gibt“ (später begründete Einstein 1948 dieses Merkmal mit einer expliziten Annahme der „Lokalität“, siehe §2.2). Costa de Beauregard war sich jedoch einer bestimmten Art von unorthodoxer Alternative zu dieser Bedingung bewusst, die ihre Rolle im EPR-Argument auf den Kopf stellte. Sein Vorschlag lautete, dass zwei entfernte Systeme „durch eine sukzessive fortschreitende und verzögerte Welle korreliert bleiben“ könnten (Costa de Beauregard 1953: 1634); das heißt, ein System könnte über eine fortschreitende Welle den Zustand der kombinierten Systeme in ihrer gemeinsamen Vergangenheit beeinflussen, die dann über eine verzögerte Welle den Zustand des entfernten Systems in einer Art „Zickzack“ durch die Raumzeit beeinflussen könnte. Auf diese Weise könnte es eine Abhängigkeit zwischen den beiden entfernten Systemen geben, ohne dass es zu einer „spukhaften Fernwirkung“ kommt. Wie Costa de Beauregard (1987b: 252) es ausdrückt:

Einstein hat natürlich Recht, wenn er eine Unvereinbarkeit zwischen seiner speziellen Relativitätstheorie und den entfernten Quantenwechselwirkungen sieht, aber nur unter der Annahme, dass fortgeschrittene Aktionen ausgeschlossen sind.

Als Costa de Beauregard 1947 seinem damaligen Vorgesetzten de Broglie diese Antwort auf das EPR-Argument vorschlug, war de Broglie „alles andere als bereit, den Vorschlag zu akzeptieren“ (1987b: 252) und verbot Costa de Beauregard, seine unorthodoxe Idee zu veröffentlichen (Price & Wharton 2015). Im Jahr 1948 hatte Feynman jedoch seine nach ihm benannten Diagramme entwickelt, in denen Antiteilchen als Teilchen interpretiert werden sollten, die sich entlang der Teilchenbahnen in der Zeit rückwärts bewegen. Daher hatte de Broglie 1953 die Veröffentlichung der Antwort von Costa de Beauregard befürwortet. Zur scheinbaren Verrücktheit des Vorschlags behauptet Costa de Beauregard: „Heute, da das Phänomen der EPR-Korrelationen experimentell sehr gut validiert ist und an sich ein ‚verrücktes Phänomen‘ ist, muss jede Erklärung dafür ‚verrückt‘ sein“ (1987b: 252; siehe auch Costa de Beauregard 1976, 1977b, 1987a).

2. Metaphysische Vorbemerkungen

Bevor auf zwei der Hauptgründe für die Annahme der Hypothese der Retrokausalität in den Grundlagen der Quantentheorie eingegangen wird, sollten einige Anmerkungen zu zwei Schlüsselbegriffen gemacht werden, die in der folgenden Diskussion eine wichtige Rolle spielen: Kausalität und Lokalität. Dies wird dazu beitragen, festzulegen, was genau mit Retrokausalität gemeint ist und was nicht.

2.1 Kausalität

Es gibt eine Tradition, die mindestens bis zu Russell (1913) zurückreicht und die leugnet, dass es in den Grundlagenwissenschaften, einschließlich der Physik, irgendeinen Platz für kausale Begriffe gibt: Der Begriff dient keinem Zweck und taucht in den Grundlagenwissenschaften einfach nicht auf. Das Argument besagt, dass die Gesetze, die das physikalische Verhalten in Grundlagenwissenschaften wie der Physik regeln, seit mindestens dem 19. Jahrhundert fast immer Differentialgleichungen sind. Solche Gleichungen sind dafür bekannt, dass sie unter bestimmten Anfangsbedingungen die genauen Eigenschaften von Systemen für alle Zeiten spezifizieren. Und wenn alles für alle Zeiten spezifiziert ist, gibt es keinen Platz mehr für Kausalität. Daher plädiert Russell dafür, „Kausalität“ aus dem Lexikon der Philosophen zu streichen, da sie sicherlich nicht Teil des wissenschaftlichen Lexikons ist.

Im Gegensatz zu Russells Position behauptet Cartwright (1979: 420), dass wir in der Wissenschaft ein kausales Vokabular brauchen und verwenden: „Kausalgesetze können nicht abgeschafft werden, da sie benötigt werden, um die Unterscheidung zwischen effektiven und ineffektiven Strategien zu begründen“. Eine der wichtigsten zeitgenössischen Darstellungen der Kausalität, die interventionistische Darstellung der Kausalität (Woodward 2003; siehe auch den Eintrag zu Kausalität und Manipulierbarkeit), ist eine Verkörperung von Cartwrights Diktum. Kurz gesagt besagt die interventionistische Darstellung, dass A eine Ursache für B ist, wenn und nur wenn die Manipulation von A ein wirksames Mittel zur (indirekten) Manipulation von B ist. Kausalität sollte im vorliegenden Artikel, sofern nicht anders angegeben, im weitesten Sinne interventionistisch verstanden werden. Nach den Darstellungen der Quantentheorie, die eine Retrokausalität annehmen, kann die Manipulation der Einstellung eines Messgeräts ein wirksames Mittel zur Manipulation von Aspekten der Vergangenheit sein. Eine weitgehend interventionistische Sichtweise der Kausalität liegt in der Tat den meisten zeitgenössischen Versuchen zugrunde, das Instrumentarium der Kausalmodellierung (siehe den Eintrag zu kausalen Modellen; Spirtes, Glymour & Scheines 2000; Pearl 2009 ) in den Grundlagen der Quantentheorie zu verwenden (Leifer & Spekkens 2013; Cavalcanti & Lal 2014; Costa & Shrapnel 2016; Allen et al. 2017).

Die Verwendung des Kausalitätsbegriffs entlang weitgehend interventionistischer Linien in den Grundlagen der Quantentheorie verpflichtet nicht zum Realismus (oder Antirealismus) in Bezug auf die fraglichen Kausalbeziehungen. Woodward verbindet Interventionismus mit Realismus in Bezug auf Kausalität, während er anerkennt:

[Es gibt] wichtige Unterschiede zwischen der Art und Weise, wie Kausalbegriffe einerseits im Alltagsverstand und in den Spezialwissenschaften vorkommen, und andererseits den empirischen Annahmen, die ihrer Anwendung in der Physik zugrunde liegen. (Woodward 2007: 67; siehe jedoch Frisch 2014: Kap. 4 und 5 für eine Antwort)

Eine weitere vorgeschlagene Strategie, um Russells Bedenken Rechnung zu tragen und gleichzeitig kausale Begriffe in der Physik weiterhin konsequent anzuwenden, besteht darin, Interventionismus in „perspektivischen“ Begriffen zu verstehen (Price 2007; Price & Corry 2007; Price & Weslake 2010; Ismael 2016). Der Perspektivismus wird in der Regel, wie es im Rahmen der modernen Physik naheliegend erscheint (obwohl dazu weiter unten noch mehr gesagt wird), im Rahmen einer Blockuniversums-Sichtweise angewendet, bei der Vergangenheit, Gegenwart und Zukunft gleichermaßen real sind. In diesem Rahmen kann Kausalität nichts mit der Veränderung der Zukunft oder der Vergangenheit zu tun haben, da beide – aus einer „externen“ Perspektive – vollständig „fixiert“ sind. Man kann Kausalität im Blockuniversum jedoch aus einer „internen“ Perspektive verstehen, nach der kausale Korrelationen genau diejenigen sind, die unter Interventionen an den Variablen, die wir als „Ursachen“ bezeichnen, stabil sind.

Der wichtige Unterschied zwischen den beiden Standpunkten – innerhalb und außerhalb des Blocks – besteht darin, dass es eine Diskrepanz zwischen den Teilen des Raumzeitblocks gibt, die aus jeder Perspektive erkenntnistheoretisch zugänglich sind. Die raumzeitlich begrenzte Perspektive, an die wir gebunden sind, erlaubt uns nur eine begrenzte erkenntnistheoretische Zugänglichkeit zu anderen raumzeitlichen Regionen. Dies ist die Perspektive, in der kausale Begriffe gemäß dem kausalen Perspektivismus perfekt anwendbar sind. Wenn wir uns andererseits als allwissende Wesen vorstellen, die epistemischen Zugang zum gesamten raumzeitlichen Block haben, sollte es nicht überraschen, dass unsere kausalen Intuitionen durcheinander geraten, wenn wir versuchen zu überlegen, wie ein raumzeitlich gebundener Akteur darüber nachdenken kann, ob er ein bestimmtes Ereignis beeinflussen soll oder nicht, das aus unserer imaginären allwissenden Perspektive bereits festgelegt ist. Nur weil wir nicht wissen, welche Ereignisse eintreten werden, und weil wir über viele andere Ereignisse nichts wissen, können wir überhaupt überlegte Akteure sein. Auch diese Überlegungen sind für die gewöhnliche Kausalität in der Zukunft ebenso relevant wie für die Kausalität in der Vergangenheit.

Viele der in §6 betrachteten retrokausalen Ansätze zur Quantentheorie lassen sich am besten mit einer Art perspektivischer interventionistischer Darstellung der Kausalität verstehen. Eine bemerkenswerte Ausnahme ist die transaktionale Interpretation (§5), bei der die Kausalität am besten im Sinne von Prozessen verstanden werden kann, die durch konservierte Mengen unterstrichen werden. Die von Kastner (2006, 2013) verteidigte possibilistische Erweiterung der transaktionalen Interpretation vermeidet darüber hinaus das Bild des Blockuniversums.

2.2 Lokalität

Gemäß dem Bellschen Theorem (Bell 1964; Clauser et al. 1969; siehe auch den Eintrag zu Bellsches Theorem) und seinen Abkömmlingen (z. B. Greenberger, Horne & Zeilinger 1989; siehe auch den Eintrag zu Bellsches Theorem, §6; Goldstein et al. 20 11; Brunner et al. 2014 für Übersichten), muss jede Theorie, die alle von der Quantentheorie vorhergesagten Korrelationen von Messergebnissen reproduziert, ein Prinzip verletzen, das Bell lokale Kausalität nennt (Bell 1976, 1990; siehe auch Norsen 2011; Wiseman & Cavalcanti 2017). In einer lokal kausalen Theorie sind die Wahrscheinlichkeiten von raumzeitlich lokalisierten Ereignissen, die in einer Region 1 auftreten, unabhängig davon, was in einer Region 2 geschieht, die räumlich von Region 1 getrennt ist, vorausgesetzt, es liegt eine vollständige Spezifikation dessen vor, was in einer Raumzeitregion 3 geschieht, die im Rückwärtslichtkegel von Region 1 liegt und die Region 1 vollständig vom Rückwärtslichtkegel von Region 2 abschirmt. (Siehe z. B. Abb. 4 und 6 in Bell 1990 oder Abb. 2 im Eintrag zu Bells Theorem.)

In einer relativistischen Umgebung beinhaltet der Begriff der Lokalität also das Verbot bedingter Abhängigkeiten zwischen räumlich getrennten Ereignissen, vorausgesetzt, dass der Bereich, von dem diese räumlich getrennten Ereignisse abhängen, ihre gemeinsame kausale (Minkowski-)Vergangenheit darstellt. Diese Charakterisierung der Lokalität geht ausdrücklich von einer kausalen Asymmetrie aus. Lokalität ist also die Vorstellung, dass es keine kausalen Beziehungen zwischen räumlich getrennten Ereignissen gibt.

Es gibt noch eine andere Bedeutung von „lokal“, die zur Vermeidung von Mehrdeutigkeiten sich ausdrücklich zu beachten lohnt. Es handelt sich um die Vorstellung, dass kausale Einflüsse kontinuierlich entlang zeitartiger Trajektorien vermittelt werden. Angesichts des Vorschlags von Costa de Beauregard, dass kausale Einflüsse „zickzackförmig“ verlaufen, ist es also durchaus möglich, dass ein retrokausales Modell von Quantenphänomenen nichtlokal in dem Sinne ist, dass kausale Beziehungen zwischen räumlich getrennten Ereignissen bestehen, aber „lokal“ in dem Sinne, dass diese kausalen Einflüsse auf zeitartige Trajektorien beschränkt sind. Zur Klarstellung: Dieser letztere Begriff lässt sich am besten als Gegensatz zu „Handlung auf Distanz“ verstehen und wird verschiedentlich als „Handlung durch Kontakt“ (Evans, Price, & Wharton 2013) oder „kontinuierliche Handlung“ (Wharton & Argaman 2020; Adlam 2022) beschrieben.

3. Motivation I: Schlupflöcher in den „No-Go-Theoremen“ ausnutzen

Der erste von zwei Hauptgründen für die Heranziehung der Retrokausalität in den Grundlagen der Quantenmechanik ergibt sich aus der Ausnutzung derselben Lücke in einer Reihe von Theoremen, die zusammen als „No-Go-Theoreme“ bekannt sind. Diesen Theoremen zufolge muss jede Theorie oder jedes Modell, das in der Lage ist, die empirisch bestätigten Konsequenzen der Quantentheorie zu erklären, zwangsläufig nichtlokal, kontextabhängig und ψ-ontisch sein (d. h. den Quantenzuständen ψ-Realität zuschreiben).

Eine Möglichkeit, die Rolle der Retrokausalität bei der Umgehung der Ergebnisse der No-Go-Theoreme zu verstehen, besteht darin, jedes Theorem als durch das sogenannte ontologische Modellgerüst untermauert zu betrachten (Harrigan & Spekkens 2010; Leifer 2014; Ringbauer 2017). Hierbei handelt es sich um einen allgemeinen Rahmen, der auf eine Vielzahl von „realistischen“ Modellen angewendet werden kann, darunter Theorien der klassischen Physik sowie lokale Ansätze mit verborgenen Variablen in der Quantenmechanik. Der Rahmen besteht aus einer operativen Beschreibung eines „Prozesses“, der beobachtete Statistiken für Messergebnisse beschreibt, die sowohl Vorbereitungen als auch Transformationen beinhalten, zusammen mit einem ontologischen Modell (oder einer „ontischen Erweiterung“), das die beobachteten Statistiken berücksichtigt. Im Quantenbereich gilt: Wenn ein Vorbereitungsverfahren einem Quantenzustand ψ entspricht, dann befindet sich ein Quantensystem, das diesem Verfahren unterzogen wird, tatsächlich in einem „ontischen“ Zustand λ, der aus einer Reihe von Zuständen Λ ausgewählt wird und die Eigenschaften des Systems vollständig spezifiziert. Der Rahmen lässt offen (und wird letztlich zur Definition verwendet), ob der Quantenzustand ψ selbst ein ontischer oder epistemischer Zustand ist (wenn ψ ontisch ist, enthält λ entweder zusätzliche ontische Freiheitsgrade oder steht in einer 1:1-Entsprechung zu ψ; siehe §3.3). Es wird angenommen, dass jede Vorbereitung über eine klassische Wahrscheinlichkeitsdichte über Λ und eine Reihe von Messverfahren, die bedingte Wahrscheinlichkeiten für von λ abhängige Ergebnisse bestimmen (wodurch das Vorbereitungsverfahren ψ ausgeblendet wird), zu einem gewissen λ führt; ausdrücklich hängt λ nicht kausal von einer zukünftigen Messeinstellung α ab. Schließlich müssen die Betriebsstatistiken die Quantenstatistik reproduzieren.

Wichtig für unsere Zwecke ist hier die Einschränkung, dass im Rahmen der ontologischen Modelle angenommen wird, dass λ als „bedingt unabhängig“ von α („Messunabhängigkeit“) angenommen wird. Diese Annahme schließt unter anderem effektiv aus, dass die zukünftige Messeinstellung α den früheren Zustand λ kausal beeinflusst. Soweit die No-Go-Theoreme durch den ontologischen Modellrahmen untermauert werden, sind sie daher nicht auf Modelle anwendbar, die eine Retrokausalität von α zu λ zulassen. Und insofern es eine Motivation gibt, die Konsequenzen der No-Go-Theoreme für die Quantentheorie zu vermeiden, ist die Retrokausalität gut geeignet, ein solches Modell zu liefern (so lautet das Argument). Insbesondere wurde argumentiert, dass die Zulassung der Retrokausalität (i) es ermöglicht, die durch die Quantentheorie bedingten Korrelationen unter Verwendung von kausalen Einflüssen durch Kontaktwirkung zu erklären (und so die Lorentz-Invarianz gewährleistet); (ii) die Annahme (bestimmter Arten von) Nichtkontextualität von vornherein als unplausibel untergräbt; und (iii) eine unabhängig attraktive ψ-epistemische Interpretation der Wellenfunktion ermöglichen könnte, die durch lokale verborgene Variablen untermauert wird. Diese Argumente werden der Reihe nach behandelt.

3.1 Nichtlokalitätstheoreme

Das Prinzip der lokalen Kausalität soll laut Bell die Idee verdeutlichen, dass

[d]ie direkten Ursachen (und Auswirkungen) von Ereignissen in der Nähe sind, und selbst die indirekten Ursachen (und Auswirkungen) nicht weiter entfernt sind als es die Lichtgeschwindigkeit zulässt. (1990: 105)

Ein Verstoß gegen dieses Prinzip deutet laut einigen Forschern, die sich mit den Grundlagen der Quantentheorie befassen, auf eine grundlegende Unvereinbarkeit zwischen der Quantentheorie und dem Geist, vielleicht sogar dem Wortlaut, der Relativitätstheorie hin (Maudlin 2011). Dass die von der Quantentheorie implizierten Korrelationen, die die lokale Kausalität verletzen, tatsächlich in der Natur vorkommen, wurde bereits mehrfach experimentell nachgewiesen (z. B. durch Freedman & Clauser 1972; Aspect, Dalibard, & Roger 1982; und Aspect, Grangier, & Roger 1982; siehe den Eintrag zu Bells Theorem, §4 für einen Überblick über frühe Experimente).

Bells Ergebnis hängt nicht nur entscheidend von der Annahme der lokalen Kausalität ab, sondern auch von der Annahme, dass die Variablen λ, die in einem bestimmten Raumzeitbereich beschrieben werden und die Bell als „lokale Beables“ bezeichnet, nicht wahrscheinlichkeitstheoretisch davon abhängen, welche Messeinstellung α einige Experimentatoren in der Zukunft dieses Bereichs wählen:

1. P(λ∣α)=P(λ).

Dies ist die oben erwähnte Annahme der Messunabhängigkeit. Sie wird manchmal auch als „kein Superdeterminismus“ bezeichnet, da sie mit einer besonders starken Form des Determinismus („Superdeterminismus“) unvereinbar ist, nach der die gemeinsame Vergangenheit der Messeinstellung α und des gemessenen Systemzustands λ beide vollständig bestimmt und eine Korrelation zwischen ihnen induziert. Wie jedoch zunächst von Costa de Beauregard (1977a) und dann von Price (1994, 1996) dargelegt wurde, ist der Superdeterminismus nicht die einzige Möglichkeit, wie Gleichung (1) verletzt werden kann: Wenn es eine Retrokausalität gibt (verstanden im Sinne einer Intervention, wie in §2.1 beschrieben), kann die Wahl der Messeinstellung α den physikalischen Zustand λ zu einem früheren Zeitpunkt kausal beeinflussen und dadurch auch Gleichung (1) falsch werden lassen. In diesem Bild, wie von Price und Wharton (2021) aufgezeigt, könnte es möglich sein, die lokalen kausalitätsverletzenden Korrelationen zwischen entfernten Ereignissen als eine Art von durch Retrokausalität verursachter „Collider-Verzerrung“ zu interpretieren.

Ohne Gleichung (1) wiederum kann der Bellsche Satz nicht mehr abgeleitet werden. Die Möglichkeit der Retrokausalität im Prinzip zuzulassen, eröffnet somit wieder die Möglichkeit, eine kausale Erklärung für die nichtlokalen Korrelationen zu geben, die durch die Quantentheorie bedingt sind, wie sie durch rein aktionsbasierte, räumlich-zeitlich zusammenhängende, Lorentz-invariante kausale Einflüsse (wie sie von Costa de Beauregard vorgesehen sind) vermittelt werden, die zwischen Systemen wirken, die durch lokale Beables beschrieben werden. Konkrete Schritte hin zu einem Modell, das dieses Versprechen erfüllen könnte, werden in §6 besprochen.

Im Gegensatz zu dieser Darstellung argumentiert Adlam (2022), dass der Versuch, die Lokalität vom Typ kontinuierliche Aktion (wie in §2.2 diskutiert) zu retten, keine gute Motivation für die Retrokausalität ist. Laut Adlam gibt es, soweit das unabhängig attraktivste Bild der Kausalität ein interventionistisches in Kombination mit einer Blockuniversumsansicht ist, keinen prinzipiellen Grund für die Annahme, dass kausale Einflüsse auf kontinuierliche Aktionen beschränkt sind. Adlam liefert ihre eigene Motivation für die Retrokausalität, basierend auf dem Argument, dass „die Akzeptanz der Existenz einer echten, unvermittelten Nichtlokalität an und für sich dazu führt, dass wir die Retrokausalität akzeptieren“ (2022: 422).

3.2 Kontextualitätstheoreme

Eine Fülle theoretischer Ergebnisse legt nahe, dass Modelle und Theorien, die die Vorhersagen der Quantentheorie reproduzieren, in gewisser Weise „kontextabhängig“ sein müssen. Ein Modell oder eine Theorie ist nicht kontextabhängig, wenn die dem System zugeschriebenen Eigenschaften (z. B. der Wert einer dynamischen Variablen, die das System aufweist) unabhängig von der Art und Weise sind, in der diese Eigenschaften gemessen oder beobachtet werden (der Kontext), über die eigentliche Beobachtung hinaus (z. B. die anderen Eigenschaften, die in Verbindung mit der Messung gemessen werden). In der klassischen Mechanik hängen die Eigenschaften, die Systeme aufweisen und die ihnen als Folge einer Messung zugeschrieben werden, im Prinzip nicht vom Messkontext ab, sodass die klassische Mechanik nicht kontextabhängig ist. Die ersten Kontextualitätssätze für die Quantentheorie gehen auf Bell (1966) sowie Kochen und Specker (1967) zurück. Sie zeigen, dass, wenn man davon ausgeht, dass Quantenmessungen die Werte beliebiger bereits vorhandener dynamischer Variablen von Quantensystemen deterministisch aufdecken, ein solches Modell kontextabhängig sein müsste (d. h., die gemessenen Werte müssten vom Kontext der Messung abhängen). Daher kann kein nichtkontextuelles deterministisches Modell mit lokalen verborgenen Variablen die beobachteten Statistiken der Quantentheorie reproduzieren.

Spekkens (2005) hat eine neue Methode entwickelt, um Kontextualität operativ zu verstehen. Unter Verwendung des ontologischen Modellrahmens ist ein ontologisches Modell einer operativen Theorie nichtkontextuell, wenn operativ äquivalente experimentelle Verfahren äquivalente Darstellungen im ontologischen Modell haben. Dieses Verständnis von Nichtkontextualität ist dann ein Prinzip der Sparsamkeit, das dem Leibniz’schen Gesetz der Identität des Ununterscheidbaren ähnelt: kein ontologischer Unterschied ohne operativen Unterschied. Mit diesem operativen Verständnis erweitert Spekkens die Klasse der ontologischen Modelle, auf die Kontextualität über deterministische lokale verborgene Variablenmodelle hinaus anwendbar ist. Aber die Geschichte ist im Wesentlichen dieselbe: Die Hypothese zugrunde liegender ontischer Eigenschaften für Quantensysteme, die nur dann unterschiedlich sind, wenn es entsprechende operative Unterschiede gibt, kann die durch die Quantentheorie bedingten Korrelationen nicht erklären. Daher kann kein nichtkontextuelles ontologisches Modell die beobachteten Statistiken der Quantentheorie reproduzieren. (Für eine ausführliche Kritik an Spekkens‘ operativem Verständnis von Kontextualität siehe Hermens 2011.)

Die Hypothese rückwirkender Einflüsse mildert diese beiden Bedenken. Durch die Retrowirkung wird die Kontextualität vom Kochen-Specker-Typ als eine Form der „kausalen Kontextualität“ potenziell erklärbar (siehe den Eintrag zum Kochen-Specker-Theorem, §5.3). Wenn es einen rückwärtsgerichteten Einfluss der gewählten Messeinstellung (und des Kontextes) auf den ontischen Zustand vor der Messung gibt, ist nicht mehr zu erwarten, dass der Messprozess einfach einen unabhängig existierenden bestimmten Wert für eine Eigenschaft des Systems aufdeckt, sondern der Messprozess kann eine kausale Rolle dabei spielen, solche Werte herbeizuführen (der Messprozess ist eher kausal als deterministisch). Tatsächlich könnte man argumentieren, dass die Kontextabhängigkeit gemessener Werte genau das ist, was man erwarten würde, wenn man retrokausale Einflüsse zulässt. Wie Wharton (2014: 203) es ausdrückt: „Die Kochen-Specker-Kontextabhängigkeit ist das Scheitern der Unabhängigkeitsannahme“, d. h. das Scheitern der Messunabhängigkeit.

In Bezug auf Spekkens‘ allgemeineres Verständnis von Kontextualität sei daran erinnert, dass es eine explizite Annahme des ontologischen Modellrahmens ist, dass der ontische Zustand unabhängig vom Messverfahren ist. Die Hypothese der Retrokausalität ist daher eine eindeutige Ablehnung des ontologischen Modellrahmens. Man könnte sich jedoch fragen, ob Spekkens‘ Prinzip der Sparsamkeit nicht so umformuliert werden könnte, dass es allgemeiner auf retrokausale Modelle anwendbar ist. §7.4 befasst sich mit einem Ergebnis von Shrapnel und Costa (2018), das darauf hindeutet, dass retrokausale Darstellungen tatsächlich eine Spekkens-artige Kontextualität akzeptieren müssen.

3.3 Psi-Ontologie-Theoreme

In einigen Modellen, die im Rahmen ontologischer Modelle dargestellt werden, ist ein ontischer Zustand λ nur mit Vorbereitungsverfahren kompatibel, die mit einem bestimmten Quantenzustand ψ verbunden sind. In diesem Fall kann ψ als Teil von λ und damit als Element der Realität selbst betrachtet werden. Modelle dieser Art werden als „ψ-ontisch“ bezeichnet. In anderen Modellen kann ein ontischer Zustand λ das Ergebnis von Vorbereitungsverfahren sein, die mit verschiedenen Quantenzuständen ψ verbunden sind. In diesen Modellen ist ψ kein Aspekt der Realität und wird oft natürlicher als unvollständiges Wissen eines Agenten über den zugrunde liegenden ontischen Zustand λ angesehen. Modelle dieser Art werden als „ψ-epistemisch“ bezeichnet. Spekkens (2007) motiviert die Suche nach attraktiven ψ-epistemischen Modellen, indem er auf verschiedene Parallelen zwischen der Quantenmechanik und einem Spielzeugmodell hinweist, bei dem das Analogon des Quantenzustands insofern erkenntnistheoretisch ist, als es unvollständige Informationen über einen zugrunde liegenden ontischen Zustand widerspiegelt.

Allerdings legen sogenannte „ψ-Ontologie-Theoreme“ (Pusey, Barrett, & Rudolph 2012; Hardy 2013; Colbeck & Renner 2012; siehe Leifer 2014 für einen Überblick) fest, dass unter bestimmten plausiblen Annahmen nur ψ-ontische Modelle die empirischen Konsequenzen der Quantentheorie reproduzieren können. Die spezifischen Annahmen, die zur Ableitung dieser Schlussfolgerung verwendet werden, unterscheiden sich für die verschiedenen Theoreme. Sie alle stützen sich jedoch auf den ontologischen Modellrahmen, der, wie bereits mehrfach erwähnt, ausdrücklich eine Annahme der Messunabhängigkeit (Gleichung (1)) beinhaltet. Da, wie oben gezeigt, die Messunabhängigkeit die Retrokausalität implizit ausschließt, gelten diese Theoreme nur insoweit, als angenommen wird, dass die Retrokausalität nicht vorhanden ist.

Darüber hinaus beruht der Satz von Pusey, Barrett und Rudolph (2012), der laut Leifer (2014) die am wenigsten anfechtbaren Annahmen von allen verwendet, auf einer zusätzlichen Unabhängigkeitsannahme, nach der die ontischen Zustände von zwei oder mehr unterschiedlichen, zufällig vorbereiteten Systemen vor der gemeinsamen Messung unkorreliert sind. Wharton (2014: 203) weist darauf hin, dass dies in einem Rahmen, der für Retrokausalität offen ist, eine problematische Annahme ist, da man dann erwarten würde, dass „Vergangenheitskorrelationen aus genau demselben Grund entstehen, aus dem zukünftige Korrelationen in Verschränkungsexperimenten entstehen“. Die Erforschung der Aussichten für retrokausale Erklärungen ist daher ein – vielleicht der – wichtige offene Weg zur Entwicklung eines attraktiven ψ-epistemischen Modells, das möglicherweise in der Lage ist, die Quantenkorrelationen zu erklären.

3.4 Klassische Ontologie?

An dieser Stelle lohnt es sich, innezuhalten und die metaphysische Motivation für einen retrokausalen Ansatz in der Quantentheorie zu betrachten, insbesondere im Hinblick auf die Umgehung dieser No-Go-Theoreme. Die orthodoxe Lesart der No-Go-Theoreme besagt, dass, was auch immer über den letztendlichen konzeptuellen und ontologischen Rahmen für das Verständnis der Quantentheorie gesagt wird, dieser nicht vollständig klassisch sein kann: Er muss nichtlokal und/oder kontextbezogen sein und/oder unbestimmten Zuständen Realität zuschreiben. Kurz gesagt: In der Quantentheorie kann es nicht um lokale verborgene Variablen gehen. Ein Teil des Reizes, angesichts dieser No-Go-Theoreme eine Retrokausalität zu postulieren, besteht darin, die (teilweise oder vollständige) Klassizität in diesem Sinne wiederzuerlangen (wenn auch mit – vielleicht nichtklassischen – symmetrischen kausalen Einflüssen). Das heißt, die Retrokausalität birgt das Potenzial, einen metaphysischen Rahmen für die Quantenmechanik zu schaffen, der kausal wirkende, kontaktbasierte, nichtkontextuelle (oder bei dem jegliche Kontextabhängigkeit durch nichtkontextuelle erkenntnistheoretische Einschränkungen untermauert wird), kontrafaktisch bestimmte, determinierte (wenn auch möglicherweise indeterministische), räumlich-zeitlich lokalisierte Eigenschaften für physikalische Systeme enthält – mit anderen Worten, eine klassische Ontologie.

Eine gute Möglichkeit, dies zu betrachten, ist die Unterscheidung von Quine (1951) zwischen der „Ontologie“ und der „Ideologie“ einer wissenschaftlichen Theorie, wobei die Ideologie einer Theorie aus den Ideen besteht, die in dieser Theorie ausgedrückt werden können. Die ideologische Ökonomie ist dann ein Maß für die Ökonomie primitiver undefinierter Aussagen, die zur Reproduktion dieser Ideologie verwendet werden. Die Behauptung hier wäre dann, dass die Ideologie symmetrischer kausaler Einflüsse ökonomischer ist als die Ablehnung einer klassischen Ontologie. Sofern die Quantenmechanik uns also etwas Tiefgreifendes über die grundlegende Natur der Realität verrät, zeigt die Hypothese der Retrokausalität, dass die Quantenmechanik nicht unbedingt lehrt, dass die Quantenontologie nicht mehr klassisch sein kann. Einige mögen dies als einen Vorzug retrokausaler Ansätze ansehen (obwohl das in Abschnitt 7.4 behandelte Shrapnel-Costa-Verbot diese Ansicht erheblich in Frage stellt.)

4. Motivation II: Zeitsymmetrie

4.1 Ableitung der Retrokausalität aus der Zeitsymmetrie

Die grundlegendsten Naturgesetze, soweit sie derzeit bekannt sind, werden im Standardmodell der Elementarteilchenphysik zusammengefasst. Diese Gesetze sind CPT-invariant, d. h. sie bleiben unter den kombinierten Operationen der Ladungsumkehr C (Ersetzen aller Teilchen durch ihre Antiteilchen), der Parität P (Umkehren der Vorzeichen aller räumlichen Koordinaten) und Zeitumkehr T gleich. Die Zeitasymmetrien, die in unserem Alltag allgegenwärtig sind, sind keine Folge einer zeitlichen Asymmetrie in diesen Gesetzen, sondern vielmehr eine Folge der Randbedingungen des Universums, insbesondere in seinen sehr frühen Stadien. Es scheint naheliegend anzunehmen, dass sich die Zeitsymmetrie der Gesetze (modulo der kombinierten Operation von C und P) auf kausale Abhängigkeiten auf der grundlegenden „ontischen“ Ebene erstreckt, die dem empirischen Erfolg der Quantentheorie zugrunde liegt. Wenn dem so ist, kann es auf dieser ontischen Ebene nicht weniger kausale Einflüsse in der Vergangenheit als in der Zukunft geben.

Price (2012) macht aus diesen skizzenhaften Überlegungen ein strenges Argument. Er zeigt, dass die Zeitsymmetrie in Kombination mit zwei Annahmen zur Quantenontologie eine Retrokausalität impliziert (im weitesten Sinne interventionistisch verstanden). Die ontologischen Annahmen sind (i) dass zumindest einige Aspekte des Quantenzustands ψ real sind (insbesondere gibt es in Prices Beispiel einen „beable“-Kodierungsphotonenpolarisationswinkel) und (ii) dass Ein- und Ausgaben von Quantenexperimenten diskrete Emissions- und Detektionsereignisse sind. Darüber hinaus ist es für Prices Argument wichtig, dass die dynamische Zeitsymmetrie (dass die dynamischen Gesetze der Theorie zeitsymmetrisch sind) so verstanden wird, dass die operative Zeitsymmetrie (dass die Menge aller möglichen Kombinationen von Vorbereitungs- und Messverfahren in einer Theorie, mit den zugehörigen Wahrscheinlichkeiten für Ausgaben bei gegebenen Eingaben, unter Austausch von Vorbereitung und Messung geschlossen ist) in ontische Zeitsymmetrie (operationelle Zeitsymmetrie plus eine geeignete Abbildung zwischen den ontischen Zustandsräumen der symmetrischen Kombinationen) übersetzt wird. Unter diesen Bedingungen muss jede grundlegende Darstellung, die die empirischen Urteile der Quantentheorie reproduziert, retrokausal sein.

Leifer und Pusey (2017) (siehe auch Leifer 2017 in Weitere Internetquellen) untermauern Prices Argument, indem sie zeigen, dass seine Annahme über die Realität (von Aspekten) des Quantenzustands ψ gelockert werden kann. Wie sie zeigen, reicht es aus, wenn Messergebnisse nur vom ontischen Zustand λ eines Systems abhängen, d. h. wenn dieser Zustand jegliche Korrelationen zwischen Vorbereitungsverfahren und Messergebnissen vollständig vermittelt („λ-Vermittlung“), damit die operationelle Zeitsymmetrie die Existenz von Retrokausalität nach sich zieht. Grundlegende Darstellungen, die wie die Bohm’sche Mechanik (Bohm 1952a,b) oder die GRW-Theorie (Ghirardi, Rimini & Weber 1986) das Postulat der Retrokausalität vermeiden, tun dies, indem sie die Zeitsymmetrie auf irgendeine Weise verletzen. Die GRW-Theorie tut dies, indem sie explizit zeitasymmetrische Dynamiken einführt. In der Bohm’schen Mechanik ist die Dynamik zeitsymmetrisch, aber die Theorie wird auf zeitasymmetrische Weise angewendet, wenn beurteilt wird, welche Quantenzustände tatsächlich realisiert werden. Insbesondere geht man davon aus, dass die Quantenzustände eines gemessenen Systems und eines damit verbundenen Messgeräts vor der Messung unkorreliert sind, während sie nach der Messung im Allgemeinen korreliert sind (Leifer & Pusey 2017: §X.).

4.2 Das Prinzip der Handlungsdualität

Die fortgeschritteneren relativistischen Quantentheorien, die der modernen Teilchenphysik zugrunde liegen, werden in der Regel im Lagrange’schen, pfadintegral-basierten Formalismus formuliert, bei dem Informationen über die Symmetrien und Wechselwirkungen der Theorie in der Aktion, S, kodiert sind. Wharton, Miller und Price (2011) verwenden diesen Formalismus als Grundlage, um zu behaupten, dass Aktionssymmetrien als ontologische Symmetrien widergespiegelt werden müssen. Wharton et al. behaupten insbesondere, dass für zwei beliebige experimentelle Anordnungen, die durch eine Raum-Zeit-Transformation (z. B. eine zeitliche Spiegelung) verbunden sind, die die Aktion unverändert lässt, die Ontologien auch über dieselbe Raum-Zeit-Transformation hinweg unverändert bleiben müssen. Dieses Prinzip, das von Wharton et al. als Aktionsdualität bezeichnet wird, erlegt realistischen Darstellungen nicht-triviale Beschränkungen auf.

Insbesondere argumentieren Evans, Price und Wharton (2013), dass es eine solche Aktionssymmetrie zwischen einem Paar verschränkter Photonen, die durch separate Polarisatoren laufen, und einem einzelnen Photon, das nacheinander durch zwei Polarisatoren läuft, gibt. Wenn die Aktionsdualität begründet ist, sollte sich die Aktionssymmetrie in identischen Ontologien für die aktionsdualen Experimente widerspiegeln. Wenn man die Aktionsdualität nicht ablehnt, bedeutet dies eines von zwei Dingen: Entweder muss die übliche kausale Erklärung für das Verhalten des einzelnen Photons in einer kausalen Erklärung für das typisch quantenmechanische Verhalten des Paares verschränkter Photonen widergespiegelt werden, und daher muss es auf der Ebene des ontischen Zustands λ eine Retrokausalität geben, oder die Nichtlokalität, die dem typischen Quantenverhalten des Paares verschränkter Photonen zugeschrieben wird, muss in ähnlicher Weise dem Verhalten des einzelnen Photons zugeschrieben werden, und somit ist die Nichtlokalität noch dramatischer verbreitet als gewöhnlich angenommen und ist in der Tat nicht nur bei verschränkten bipartiten Quantensystemen zu finden. Insofern es ein starkes Argument für das Verhalten eines einzelnen Photons gibt, das nacheinander zwei Polarisatoren passiert, und das eine vollkommen gute kausale Erklärung auf der Grundlage räumlich-zeitlich lokalisierter Eigenschaften hat, ist das Argument von Evans et al., dass dies ein ebenso starkes Argument für die Retrokausalität in der Quantentheorie ist.

5. Die transaktionale Interpretation

In diesem Beitrag wurden bisher die beiden wichtigsten Argumente für die Annahme der Retrokausalität als Hypothese für den Umgang mit den interpretatorischen Herausforderungen der Quantentheorie betrachtet. Diese Motivationen allein reichen jedoch nicht aus, um eine Interpretation oder ein Modell der Quantentheorie zu erstellen. §6 besteht aus einer Übersicht über eine Reihe von retrokausalen Modellen, aber in diesem Abschnitt wird zunächst das vielleicht prominenteste retrokausale Modell betrachtet, die Transaktionsinterpretation. Die von Cramer in den 1980er Jahren entwickelte Transaktionsinterpretation (Cramer 1980, 1986, 1988) ist stark vom Rahmen des Wheeler-Feynman-Absorber-Ansatzes zur Elektrodynamik (siehe §1) beeinflusst; das Wheeler-Feynman-Schema kann zur Beschreibung des mikroskopischen Austauschs eines einzelnen Quants von Energie, Impuls usw. usw. zwischen und innerhalb von Quantensystemen verwendet werden.

Im Mittelpunkt der Transaktionsinterpretation steht die „Transaktion“: Reale physikalische Ereignisse werden mit sogenannten „Handshakes“ zwischen sich vorwärts entwickelnden Quantenzuständen ψ und sich rückwärts entwickelnden komplex Konjugierten ψ∗ identifiziert. Wenn ein Quantenemitter (z. B. ein vibrierendes Elektron oder ein Atom in einem angeregten Zustand) ein einzelnes Quant (in diesen Fällen ein Photon) emittieren soll, erzeugt die Quelle ein Strahlungsfeld – die „Angebotswelle“. Analog zur Wheeler-Feynman-Beschreibung breitet sich dieses Feld sowohl vorwärts als auch rückwärts in der Zeit (sowie im Raum) aus. Wenn dieses Feld auf einen Absorber trifft, wird ein neues Feld erzeugt – die „Bestätigungswelle“ –, das sich ebenfalls sowohl vorwärts als auch rückwärts in der Zeit ausbreitet und somit zum Zeitpunkt der Emission als vorgezogene einfallende Welle am Emitter vorhanden ist. Sowohl das vom Absorber erzeugte verzögerte Feld als auch das vom Emitter erzeugte vorauseilende Feld heben sich mit dem vom Emitter erzeugten verzögerten Feld und dem vom Absorber erzeugten vorauseilenden Feld für alle Zeiten vor der Emission und nach der Absorption des Photons exakt auf; nur zwischen dem Emitter und dem Absorber gibt es ein Strahlungsfeld. Somit wird die Transaktion mit diesem „Handschlag“ abgeschlossen: ein Zyklus von Angebots- und Bestätigungswellen, der

wiederholt [wird], bis die Antwort des Emitters und des Absorbers ausreicht, um alle Quanten-Randbedingungen zu erfüllen … an diesem Punkt ist die Transaktion abgeschlossen. (Cramer 1986: 662)

Viele Bestätigungswellen von potenziellen Absorbern können zum Zeitpunkt der Emission auf den Emitter treffen, aber die Quantenrandbedingungen lassen normalerweise nur die Bildung einer einzigen Transaktion zu. Jeder Beobachter, der diesen Prozess miterlebt, würde nur die abgeschlossene Transaktion wahrnehmen, die als Durchgang eines Teilchens (z. B. eines Photons) zwischen Emitter und Absorber interpretiert würde.

Die transaktionale Interpretation geht davon aus, dass die Wellenfunktion eine reale physische Welle mit räumlicher Ausdehnung ist. Die Wellenfunktion des quantenmechanischen Formalismus ist identisch mit der anfänglichen Angebotswelle des Transaktionsmechanismus und die kollabierte Wellenfunktion ist identisch mit der abgeschlossenen Transaktion. Quantenpartikel sind daher nicht als durch die Wellenfunktion dargestellt zu betrachten, sondern vielmehr als durch die abgeschlossene Transaktion, von der die Wellenfunktion nur die Anfangsphase ist. Wie Cramer erklärt:

Die Transaktion kann einen einzelnen Emitter und Absorber oder mehrere Emitter und Absorber umfassen, ist jedoch nur dann vollständig, wenn an allen Emissions- und Absorptionsorten geeignete Randbedingungen erfüllt sind. Übertragene Teilchen haben keine eigene Identität, die unabhängig von der Erfüllung dieser Randbedingungen ist. (1986: 666)

Die Amplitude der Bestätigungswelle, die vom Absorber erzeugt wird, ist proportional zur lokalen Amplitude der einfallenden Welle, die sie stimuliert hat, und diese wiederum hängt von der Dämpfung ab, die sie auf ihrem Weg von der Quelle erhalten hat. Somit ist die Gesamtamplitude der Bestätigungswelle nur das absolute Quadrat der ursprünglichen Angebotswelle (am Absorber bewertet), was die Born’sche Regel ergibt. Da die Born’sche Regel als Produkt des Transaktionsmechanismus entsteht, kommt der Rolle des Beobachters bei der Messung keine besondere Bedeutung zu. Der „Zusammenbruch der Wellenfunktion“ wird als Abschluss der Transaktion interpretiert.

Die transaktionale Interpretation interpretiert den Quantenzustand ψ ausdrücklich als real und stellt daher keinen Versuch dar, die Schlupflöcher der Retrokausalität in den Theoremen auszunutzen, die ψ-epistemische Erklärungen ausschließen. Darüber hinaus untergräbt die transaktionale Interpretation das Dilemma im Kern des EPR-Arguments (Einstein et al. 1935), indem sie zulässt, dass inkompatible Observable gleichzeitig bestimmte Werte annehmen: Die Wellenfunktion, so die transaktionale Interpretation,

bringt jedem potenziellen Absorber die gesamte Bandbreite möglicher Ergebnisse, und alle haben eine „simultane Realität“ im Sinne der EPR. Der Absorber interagiert so, dass eines dieser Ergebnisse in der Transaktion entsteht, sodass die kollabierte [Wellenfunktion] nur eines dieser Ergebnisse manifestiert. (Cramer 1986: 668).

Am wichtigsten ist jedoch, dass die transaktionale Interpretation sowohl verzögerte als auch fortgeschrittene Wellen verwendet und damit die Möglichkeit einer „Zickzack“-Erklärung der Nichtlokalität im Zusammenhang mit verschränkten Quantensystemen zulässt.

Bevor wir uns einem der bedeutenderen Einwände gegen die transaktionale Interpretation und die Retrokausalität im Allgemeinen zuwenden, ist es aufschlussreich, hier zwei sich ergänzende Beschreibungen dieses Transaktionsprozesses auseinanderzunehmen. Einerseits gibt es eine Beschreibung des realen physikalischen Prozesses, der aus dem Durchgang eines Teilchens zwischen Emitter und Absorber besteht und den ein zeitlich gebundener Experimentator beobachten würde; und andererseits gibt es eine Beschreibung eines dynamischen Prozesses von Angebots- und Bestätigungswellen, der für die Durchführung der Transaktion von entscheidender Bedeutung ist. Dieser letztere Prozess kann einfach nicht in einer gewöhnlichen zeitlichen Abfolge stattfinden, nicht zuletzt, weil jeder zeitlich gebundene Beobachter von Natur aus keine Angebots- oder Bestätigungswellen erkennen kann. Cramer schlägt vor, den „dynamischen Prozess“ als in einer „Pseudozeit“-Sequenz ablaufend zu verstehen:

Der hier vorgestellte Bericht über eine Emitter-Absorber-Transaktion verwendet das semantische Mittel, einen Prozess zu beschreiben, der sich über ein licht- oder zeitähnliches Intervall der Raumzeit erstreckt, als ob er in einer Zeitfolge außerhalb des Prozesses stattfinden würde. Der Leser wird daran erinnert, dass dies nur eine pädagogische Konvention zum Zweck der Beschreibung ist. Der Prozess ist zeitlos und die einzigen Beobachtungen stammen aus der Überlagerung aller „Schritte“ zur Bildung der endgültigen Transaktion. (Cramer 1986: 661, fn.14)

Diese Schritte sind natürlich der sich zyklisch wiederholende Austausch von Angebots- und Bestätigungswellen, die so lange andauern, „bis der Nettoaustausch von Energie und anderen konservierten Größen die Quantenrandbedingungen des Systems erfüllt“ (1986: 662). Hier besteht ein starkes Gefühl dafür, dass jeder Prozess, der als in der Pseudozeit ablaufend beschrieben wird, überhaupt kein Prozess ist, sondern, wie Cramer erinnert, lediglich eine „pädagogische Konvention zum Zwecke der Beschreibung“. Ob es am besten ist, Kausalität gemäß der transaktionalen Interpretation in Form von Prozessen zu verstehen, die durch konservierte Mengen unterstrichen werden, hängt eng damit zusammen, wie man diesen pseudotemporalen Prozess am besten verstehen sollte.

Maudlin (2011) skizziert eine Auswahl von Problemen, die in Cramers Theorie als Ergebnis der pseudotemporalen Darstellung des Transaktionsmechanismus auftreten: Prozesse, die für den Abschluss einer Transaktion wichtig sind, finden nur in Pseudozeit (und nicht in Echtzeit) statt und können daher nicht als überhaupt stattgefunden bezeichnet werden. Da ein zeitlich gebundener Beobachter immer nur eine abgeschlossene Transaktion wahrnehmen kann, d. h. eine kollabierte Wellenfunktion, existiert die nicht kollabierte Wellenfunktion nie wirklich. Da die anfängliche Angebotswelle mit der Wellenfunktion des Quantenformalismus identisch ist, existiert laut Maudlin auch kein nachfolgender Austausch von fortgeschrittenen und verzögerten Wellen, der erforderlich ist, um die quantenmechanischen Wahrscheinlichkeiten zu liefern. Darüber hinaus scheint Cramers Darstellung des Transaktionsmechanismus darauf hinzudeuten, dass die Stimulation sequenzieller Angebots- und Bestätigungswellen deterministisch erfolgt, was eine klaffende Lücke in jeder Erklärung hinterlässt, die die transaktionale Interpretation der stochastischen Natur der Quantenmechanik liefern könnte. Obwohl diese Probleme erheblich sind, räumt Maudlin ein, dass sie tatsächlich nur für Cramers Theorie gelten könnten. Maudlin bringt auch einen allgemeineren Einwand gegen retrokausale Modelle der Quantenmechanik vor, die seiner Meinung nach ein Problem für „jede Theorie darstellen, in der sowohl rückwärts als auch vorwärts gerichtete Einflüsse zusammenwirken, um Ereignisse zu formen“ (2011: 184).

Maudlins Haupteinwand gegen die Transaktionsinterpretation hängt mit der Tatsache zusammen, dass der Transaktionsprozess entscheidend von der Unveränderlichkeit der Absorber abhängt, die „einfach in der Zukunft da draußen sitzen und darauf warten, zu absorbieren“ (2011: 182); man kann nicht davon ausgehen, dass gegenwärtige Ereignisse die zukünftige Disposition der Absorber nicht beeinflussen können. Maudlin bietet ein Gedankenexperiment an, um diesen Einwand zu veranschaulichen. Eine radioaktive Quelle ist darauf beschränkt, ein β-Teilchen entweder nach links oder nach rechts abzustrahlen. Rechts befindet sich der Absorber A in einer Entfernung von 1 Einheit. Der Absorber B befindet sich ebenfalls rechts, jedoch in einer Entfernung von 2 Einheiten, und ist auf Drehzapfen montiert, sodass er auf Befehl nach links geschwenkt werden kann. Ein β-Teilchen, das zum Zeitpunkt t₀ nach rechts ausgesendet wird, wird zum Zeitpunkt t₁ vom Absorber A absorbiert. Wenn das β-Teilchen nach dem Zeitpunkt t₁ nicht am Absorber A nachgewiesen wird, wird der Absorber B schnell nach links geschwenkt, um das β-Teilchen nach dem Zeitpunkt 2t₁ nachzuweisen.

Gemäß der transaktionalen Interpretation werden, da es zwei mögliche Ergebnisse gibt (Erkennung bei Absorber A oder Erkennung bei Absorber B), zwei Bestätigungswellen aus der Zukunft zurückgesendet, eine für jeden Absorber. Da es außerdem gleich wahrscheinlich ist, dass das β-Teilchen an einem der beiden Absorber erkannt wird, sollten die Amplituden dieser Bestätigungswellen gleich sein. Eine Bestätigungswelle von Absorber B kann jedoch nur dann zum Emitter zurückgesendet werden, wenn sich Absorber B links befindet. Damit dies der Fall ist, darf Absorber A das β-Teilchen nicht erkannt haben und somit muss das Ergebnis des Experiments bereits entschieden sein. Das Eintreffen einer Bestätigungswelle von Absorber B beim Emitter sorgt dafür, dass das β-Teilchen-Teilchen nach links geschickt wird, obwohl die Amplitude dieser Welle eine Wahrscheinlichkeit von nur der Hälfte dafür impliziert. Wie Maudlin (2011: 184) so treffend feststellt: „Cramers Theorie bricht zusammen“.

Die zentrale Herausforderung von Maudlin besteht darin, dass jeder rückwirkende Mechanismus sicherstellen muss, dass das zukünftige Verhalten des Systems im Einklang mit der raumzeitlichen Struktur steht, die durch alle möglichen zukünftigen Ursachen vorgegeben wird: „Stochastische Ergebnisse zu einem bestimmten Zeitpunkt können die Zukunft beeinflussen, aber diese Zukunft selbst soll eine Rolle bei der Erzeugung der Ergebnisse spielen“ (2011: 181). In der transaktionalen Interpretation setzt die Existenz der Bestätigungswelle selbst einen bestimmten zukünftigen Zustand des Systems mit rückwirkendem Einfluss voraus. Bei standardmäßigen (d. h. zeitlich vorwärts gerichteten) stochastischen kausalen Einflüssen, die die Zukunft von der Gegenwart aus beeinflussen, ist eine bestimmte Zukunft jedoch nicht unbedingt in jedem Fall garantiert, wie Maudlins Experiment zeigt.

Maudlins Infragestellung der transaktionalen Interpretation hat zu einer Reihe von Reaktionen geführt (siehe P. Lewis 2013 und den Eintrag zu Fernwirkung in der Quantenmechanik für weitere Diskussionen über mögliche Reaktionen). Die Antworten lassen sich im Allgemeinen in zwei Typen einteilen (P. Lewis 2013). Der erste Antworttyp versucht, Maudlins Beispiel in die transaktionale Interpretation einzubeziehen. Berkovitz (2002) verteidigt die transaktionale Interpretation, indem er zeigt, dass Kausalschleifen, wie sie in Maudlins Experiment gefunden wurden, nicht den Annahmen über Wahrscheinlichkeiten gehorchen müssen, die in linearen kausalen Situationen üblich sind. Marchildon (2006) schlägt vor, die Absorptionseigenschaften der Randbedingungen über große Entfernungen zu berücksichtigen: Wenn das Universum ein perfekter Absorber für alle Strahlung ist, dann wird eine Bestätigungswelle von links zum Zeitpunkt der Emission immer von der radioaktiven Quelle empfangen und die korrekte Wahrscheinlichkeitsinformation kodieren. Kastner (2006) schlägt vor, zwischen konkurrierenden Anfangszuständen der radioaktiven Quelle zu unterscheiden, die den beiden Emissionsmöglichkeiten entsprechen und zusammen einen instabilen Verzweigungspunkt zwischen verschiedenen Welten charakterisieren, wobei die scheinbar problematischen Wahrscheinlichkeiten eine probabilistische Struktur in beiden möglichen Welten widerspiegeln.

Die zweite Art der Reaktion besteht darin, die transaktionale Interpretation zu modifizieren. Zum Beispiel führt Cramer (2016) die Idee einer Hierarchie von Echos fortgeschrittener Wellen ein, die von der Größe des raumzeitlichen Intervalls abhängt, aus dem sie stammen. Kastner (2013) vermutet jedoch, dass die Ursache des von Maudlin aufgedeckten Problems in der Vorstellung liegt, dass Quantenprozesse in der „Blockwelt“ stattfinden, und lehnt diese Auffassung von Prozessen in ihrer eigenen Entwicklung der transaktionalen Interpretation ab. Gemäß ihrer „possibilistischen“ transaktionalen Interpretation existieren alle potenziellen Transaktionen in einem realen Raum der Möglichkeiten, was gleichzeitig eine Art modalen Realismus und eine Unbestimmtheit in Bezug auf zukünftige Zustände des Systems bedeutet (daher Kastners Ablehnung der Blockuniversums-Sichtweise). Die possibilistische Transaktionsinterpretation behandelt Mehrteilchenszenarien wohl natürlicher und stellt die modernste nachhaltige Entwicklung der Transaktionsinterpretation dar (obwohl in P. Lewis 2013 Kritik an der possibilistischen Transaktionsinterpretation geäußert wird, die spezifisch für Maudlins Herausforderung ist).

6. Entwicklungen hin zu einem retrokausalen Modell

Die transaktionale Interpretation mag als das bekannteste – und historisch bedeutendste – retrokausale Modell auf dem Markt gelten, aber es ist nicht das einzige. Während die Retrokausalität in der Quantenmechanik im Laufe der Jahre Gegenstand zahlreicher Analysen und Kritik war (Rietdijk 1978; Sutherland 1983, 1985, 1989; Price 1984, 2001; Hokkyo 1988, 2008; Miller 1996, 1997; Atkinson 2000; Argaman 2010; Evans 2015) liegt der Schwerpunkt dieses Abschnitts auf einer Überprüfung einiger konkreterer Vorschläge für retrokausale Modelle.

6.1 Der Zwei-Zustands-Vektor-Formalismus

Der heute als Zwei-Zustands-Vektor-Formalismus bekannte Ansatz wurde erstmals von Watanabe (1955) vorgeschlagen und dann von Aharonov, Bergmann und Lebowitz (1964) wiederentdeckt. Der Vorschlag besagt, dass der übliche, sich vorwärts entwickelnde Quantenzustand nicht genügend Informationen enthält, um ein Quantensystem vollständig zu spezifizieren; vielmehr muss der sich vorwärts entwickelnde Zustand durch einen sich rückwärts entwickelnden Zustand ergänzt werden, um eine vollständige Spezifikation zu erhalten. Gemäß dem Zweizustandsvektorformalismus enthält die vollständige Quantenbeschreibung also einen Zustandsvektor, der sich in der Zeit von der anfänglichen Randbedingung in die Zukunft vorwärts entwickelt, und einen Zustandsvektor, der sich in der Zeit von der zukünftigen Randbedingung in die Vergangenheit rückwärts entwickelt. Nur eine Kombination aus vollständigen Messungen an den Anfangs- und Endgrenzen kann eine vollständige Spezifikation eines Quantensystems liefern. Der Zwei-Zustandsvektor-Formalismus ist empirisch äquivalent zur Standard-Quantenmechanik (Aharonov & Vaidman 1991, 2008).

Der Schwerpunkt des zweizustandsvektorförmlichen Formalismus liegt auf den operativen Elementen der Theorie, und es gibt nur sehr wenige ontologische Vorschriften – einschließlich der Frage, wie Kausalität am besten zu verstehen ist. Er ist im Prinzip mit einer Vielzahl ergänzter retrokausaler Ontologien kompatibel, z. B. dem kausal symmetrischen Bohm-Modell (§6.3).

6.2 Spielzeugmodelle

Spielzeugmodelle wurden verwendet, um zu veranschaulichen, wie Retrokausalität möglicherweise realisiert werden könnte. Price (2008) schlägt ein einfaches Spielzeugmodell mit verbundenen Knoten vor, die unterschiedliche Werte annehmen können, das er als „Helsinki-Modell“ bezeichnet. Wenn man die Knoten als teilweise zeitlich geordnet und die Werte der exogenen Randknoten als steuerbar interpretiert, beinhaltet die von Price spezifizierte Dynamik eine kausale Bidirektionalität, d. h. sowohl gewöhnliche Vorwärtskausalität als auch Retrokausalität, die in einem interventionistischen Sinne verstanden wird. Obwohl das Modell tatsächlich ein bestimmtes Verhalten aufweist, das natürlich als retrokausal interpretiert werden kann, ist eine vollständige Analogie zur Standard-Quantenmechanik begrenzt.

Das Helsinki-Modell besteht aus drei primitiven endogenen Knoten, wobei jeder Knoten einen Treffpunkt von drei Kanten umfasst, mit zwei „internen“ Kanten, die die drei Knoten verbinden, und fünf „externen“ Kanten. Jede Kante hat eine von drei „Geschmacksrichtungen“, A, B oder C. Das System ist zeitlich orientiert und verfügt über drei exogene Knoten, die jeweils mit einer einzelnen Kante verbunden sind und die „Eingaben“ des Systems (Vorbereitungen/Eingriffe) darstellen, sowie über zwei „Ausgaben“ des Systems (Messergebnisse/Beobachtungen), die mit den verbleibenden zwei Kanten verbunden sind. Die beiden inneren Kanten stehen für verborgene Geschmacksrichtungen, die nicht direkt kontrolliert oder beobachtet werden können. Es gibt zwei Grundregeln, die die Dynamik dieses Spielzeugsystems bestimmen: (i) jeder Knoten muss streng inhomogen sein – d. h. er umfasst drei Kanten unterschiedlicher Geschmacksrichtungen – oder streng homogen – d. h. drei Kanten derselben Geschmacksrichtung, und (ii) aufeinanderfolgende homogene Knoten sind verboten.

Das retrokausale Verhalten des Modells ergibt sich aus den starken Einschränkungen, die die beiden Grundregeln für die möglichen Geschmacksrichtungen der verborgenen Kanten vorsehen, wodurch Korrelationen zwischen den Eingangszuständen und den verborgenen Zuständen hergestellt werden. Somit beeinflussen Eingriffe in die linken oder rechten exogenen Variablen den vollständigen Satz möglicher verborgener Zustände des Systems. Unter der Annahme, dass die verborgenen Zustände in der Vergangenheit dieser variablen Entscheidungen liegen, hängt der verborgene Zustand „retrokausal“ von den linken und rechten Eingangseinstellungen ab. Darüber hinaus führen bei bestimmten Knotenvariablen einige Eingriffe in die linken oder rechten exogenen Variablen zu Eingriffen in die entfernte Ausgabevariable, was eine Art Nichtlokalität anzeigt (aber die Nicht-Signalisierung verletzt).

Ehrgeiziger ist Corry (2015), der drei Spielzeugmodelle vorschlägt, die ebenfalls Knoten und Verbindungen verwenden, Bellsche Korrelationen aufweisen und diese auf rein lokale Weise erklären, indem die Knotenbeschränkungen nur auf Informationen verweisen, die an den jeweiligen Knoten verfügbar sind. Die Modelle geben jedoch im Allgemeinen keine Werte für nicht beobachtete Knoten an. Als Ausweg schlägt Corry vor, solche Werte entweder zu postulieren, wobei man „retro-finkische Dispositionen“ in Kauf nehmen muss (Dispositionen, die, wenn sie ausgelöst würden, gar nicht erst vorhanden wären), oder die Existenz solcher Werte einfach rundheraus zu leugnen.

6.3 Das kausal-symmetrische Bohm-Modell

Ein Modell, das die Hypothese der Retrokausalität aufstellt und die Konsequenzen der Standard-Quantentheorie reproduziert, ohne die Lorentz-Invarianz zu verletzen, ist Sutherlands (2008, 2015, 2017) kausal symmetrische Version der Bohmschen Mechanik. Dieses Modell fügt dem Standard-Quantenzustand ψ_i der gewöhnlichen Bohmschen Mechanik, der durch eine Anfangsrandbedingung festgelegt ist, einen zusätzlichen Quantenzustand ψ_f hinzu, der durch eine Endrandbedingung festgelegt ist. Sutherland leitet ein Analogon zur „Führungsgleichung“ für die Teilchenbewegung in der gewöhnlichen Bohmschen Mechanik ab, das in Bezug auf diese Zustände symmetrisch ist. Die Nullkomponente des Wahrscheinlichkeitsstroms, der in direktem Zusammenhang mit der Wahrscheinlichkeitsdichte steht, wird wie folgt berechnet (Gleichung 2):

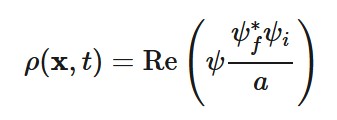
Wobei (Gleichung 3):

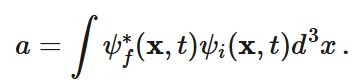
Schließlich verlangt das Modell aus Gründen der Konsistenz auch, dass die bedingte Wahrscheinlichkeit, dass der Endzustand ψ_f ist, gegeben den Anfangszustand ψ_i, lautet (Gleichung 4):

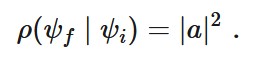
Berkovitz (2008) kritisiert die Verwendung der zusätzlichen Annahme-Gleichung (4) und die Notwendigkeit dieser Annahme in Sutherlands Modell und argumentiert, dass sie zu einer unerwünschten Form von Kausalschleifen führt und einen ad hoc Charakter hat, da es keinen unabhängigen Grund gibt, zu glauben, dass ψ_i und ψ_f
auf diese Weise korreliert sein sollten.

Sutherlands Modell ist insofern ausdrücklich retrokausal, als die Teilchendynamik von ψ_f beeinflusst wird,
was wiederum von der zukünftigen Messeinstellung abhängt. Es enthält auch kausale Einflüsse durch Kontakt, da Bell’sche Korrelationen auf die von Costa de Beauregard vorgesehene „Zickzack“-Weise berücksichtigt werden, wie in §1 beschrieben.

6.4 Die relationale Blockwelt-Interpretation

Silberstein, Stuckey und McDevitt (2018) schlagen auf der Grundlage früherer Arbeiten zusammen mit Cifone (Stuckey, Silberstein und Cifone 2008; Silberstein, Cifone und Stuckey 2008) eine realistische Interpretation vor, die sie als „relationale Blockwelt-Sichtweise“ bezeichnen. Die Ontologie dieser Interpretation besteht aus sogenannten „Raum-Zeit-Quellen-Elementen“, die als „Amalgam aus Raum, Zeit und Quellen“ charakterisiert werden (Silberstein, Stuckey, & McDevitt 2018: 153).

Technisch gesehen ist der relationale Blockwelt-Ansatz als eine Modifikation der Gittereich-Theorie angelegt, wobei das Feynman-Pfadintegral als „adynamische globale Einschränkung“ fungiert. Obwohl eher adynamisch und akausal als retrokausal, nutzt diese Interpretation nach Ansicht der Autoren die retrokausalen Schlupflöcher der No-Go-Theoreme aus. Sie verstehen die relationale Blockwelt-Sichtweise als ψ-epistemisch. In neueren Arbeiten (2018: Kap. 6) haben Silberstein, Stuckey und McDevitt diesen Ansatz zu einem ehrgeizigen übergreifenden Programm in der Grundlagenphysik weiterentwickelt, das auf eine feldtheoretische Vereinheitlichung sowie eine neuartige Darstellung der Quantengravitation abzielt.

6.5 Das Modell der doppelten Grenzwerte

Schulman (1997, 2012) schlägt eine Lösung für das Problem der Quantenmessung vor, die auf der Möglichkeit einer zukünftigen Konditionierung basiert und aus seiner Analyse des thermodynamischen Zeitpfeils stammt. Ausgehend von Loschmidts Herausforderung an Boltzmann, dass es nicht möglich sein sollte, irreversibles dynamisches Verhalten aus zeitsymmetrischer Dynamik abzuleiten (siehe den Eintrag zur thermodynamischen Asymmetrie in der Zeit), stellt Schulman fest, dass eine erfolgreiche „Rückwärtsvorhersage“ vergangener makroskopischer Zustände eines thermodynamischen Systems in der Tat asymmetrisch zu einer erfolgreichen „Vorhersage“ zukünftiger makroskopischer Zustände ist. Für eine erfolgreiche Retrodiktion wird nicht jeder der mikroskopischen Zustände eines makroskopischen Zustands gemäß den dynamischen Gesetzen entwickelt (was mit dem Vorhersageprozess identisch ist und die Grundlage für Loschmidts Herausforderung bildet), sondern stattdessen ein vorheriger makroskopischer Zustand angenommen, auf den der Vorhersageprozess angewendet werden kann, sodass der aktuelle makroskopische Zustand des Systems angesichts der dynamischen Entwicklung der vorherigen mikroskopischen Zustände mit hoher Wahrscheinlichkeit erreicht wird. Da die Entwicklung der überwiegenden Mehrheit (nach dem Liouville-Maß) dieser Zustände gemäß den dynamischen Gesetzen zu Trajektorien führt, die mit der Retrodiktionshypothese in Konflikt stehen, werden diese Zustände im Retrodiktionsprozess zugunsten der wenigen speziellen mikroskopischen Zustände, die der dynamischen Entwicklung akzeptabler hypothetischer Anfangsbedingungen entsprechen, effektiv verworfen.

Schulmans Vorschlag als Reaktion auf diese Asymmetrie lautet, dass ebenso wie die Menge der möglichen endgültigen mikroskopischen Zustände für eine erfolgreiche Rückführung eingeschränkt werden muss, auch die zulässigen anfänglichen mikroskopischen Zustände für die Zwecke der Vorhersage eingeschränkt werden sollten. Da die endgültigen mikroskopischen Zustände von dem vergangenen Zustand des Systems abhängig sind, sind die anfänglichen mikroskopischen Zustände von dem zukünftigen Zustand des Systems abhängig – eine Abhängigkeit, die in thermodynamischen Prozessen verborgen ist, bei denen die mikroskopischen Zustände des Systems makroskopisch nicht unterscheidbar sind. Diese zukünftige Abhängigkeit ist ein zentrales Merkmal von Schulmans Vorschlag der zweifachen Randbedingung, und die verborgene Natur dieser Abhängigkeit nennt Schulman „kryptische Einschränkungen“.

In Bezug auf die Quantentheorie behauptet Schulman, dass Quantenüberlagerungen makroskopisch unterschiedlicher Zustände, die durch die Quantenentwicklung erzeugt werden und die im Mittelpunkt vieler nichtklassischer Elemente der Quantentheorie stehen, das sind, was er als „groteske“ Zustände bezeichnet, und schlägt vor, dass diese Zustände in Quantensystemen aufgrund zukünftiger Konditionierung und kryptischer Einschränkungen vermieden werden. Genauso wie es spezielle mikroskopische Zustände thermodynamischer Systeme gibt, die sich „entgegen“ dem zweiten Hauptsatz der Thermodynamik entwickeln (die im Prozess der Rückwärtsvorhersage identifiziert werden), muss es auch „spezielle“ mikroskopische Zustände eines Quantensystems geben, die nicht zu grotesken Zuständen führen, wenn sie sich gemäß den quantendynamischen Gesetzen entwickeln, sondern diese Zustände führen zu einem bestimmten definierten Zustand der Superposition. Schulmans Lösung für das Problem der Quantenmessung besteht darin, dass bei jedem durchgeführten Experiment die Anfangsbedingungen des Quantensystems zu diesen speziellen Zuständen gehören, die durch reine unitäre Quantenentwicklung zu einem einzigen Ergebnis des Experiments führen (Schulman 1997: 214). Groteske Zustände, die problematischen Zustände des Quantenmessproblems, werden somit vermieden.

Schulmans Vorschlag geht implizit davon aus, dass bei der Vorbereitung eines Experiments nur der makroskopische Zustand des Systems unter der Kontrolle des Experimentators steht; es ist unmöglich, den genauen mikroskopischen Zustand zu kontrollieren. Schulman geht davon aus, dass dieser anfängliche mikroskopische Zustand immer ein besonderer Zustand ist. Schulman sieht die Einschränkung des besonderen Zustands in Zusammenhang mit zukünftigen Bedingungen, und da diese Einschränkungen für den Experimentator erst dann ersichtlich sind, wenn die zukünftigen Bedingungen am Ende des Experiments „gemessen“ werden, sind diese Einschränkungen kryptisch. Aufgrund der zukünftigen Konditionierung der Anfangszustände ist Schulmans Vorschlag eine Art rückwirkender Mechanismus, der in einem interventionistischen Sinne verstanden wird. (Für eine Erweiterung von Schulmans Modell in das Lagrange-Schema (§6.6) siehe Almada et al. 2016 und Wharton 2014, 2018.)

6.6 „All-at-once“-Lagrange-Modelle

Wharton (2010a; siehe auch Wharton 2007, 2010b, 2013, 2016, 2018; Wharton, Miller, & Price 2011; Evans, Price, & Wharton 2013) schlägt eine „neue Interpretation der Klein-Gordon-Gleichung“ für ein neutrales, spinloses relativistisches Teilchen vor. Der Bericht ist ein retrokausales Bild, das auf dem Hamiltonschen Prinzip und der symmetrischen Beschränkung sowohl der Anfangs- als auch der Endrandbedingungen basiert, um Bewegungsgleichungen aus einem Lagrange-Modell zu konstruieren, und ist ein natürlicher Rahmen für eine perspektivische interventionistische Darstellung der Kausalität. Wharton behandelt externe Messungen als physikalische Beschränkungen, die einem System auferlegt werden, genauso wie Randbedingungen dem Aktionsintegral des Hamiltonschen Prinzips auferlegt werden; die abschließende Messung offenbart nicht einfach bereits vorhandene Werte der Parameter, sondern schränkt diese Werte ein (genau wie die anfängliche Randbedingung). Das Wharton-Modell wurde als „All-at-once“-Ansatz beschrieben, da die Dynamik physikalischer Systeme zwischen einer Anfangs- und einer Endgrenze en bloc als Lösung eines Zwei-Zeit-Randwertproblems entsteht.

Bei dieser Interpretation betrachtet man die Realität ausschließlich zwischen zwei zeitlichen Grenzen als durch ein klassisches Feld ϕ beschrieben, das eine Lösung der Klein-Gordon-Gleichung ist: Die Angabe von Feldwerten sowohl an einer Anfangs- als auch an einer Endgrenze (im Gegensatz zu Feldwerten und ihrer Änderungsrate nur an der Anfangsgrenze) schränkt die Feldlösungen zwischen den Grenzen ein. Wharton argumentiert, dass die Einschränkung solcher Felder sowohl an einer Anfangs- als auch an einer Endgrenze (oder einer geschlossenen Hyperebene in der Raumzeit) zwei auffällige Quantenmerkmale erzeugt: die Quantisierung bestimmter Feldeigenschaften und die Kontextabhängigkeit der unbekannten Parameter, die das Feld zwischen den Grenzen charakterisieren. (Dass es vor der Auferlegung der Endbedingung unbekannte Parameter gibt, ist durch die Unterbestimmung des klassischen Feldes gewährleistet, da in den Anfangsdaten nur die Feldwerte und nicht deren Änderungsrate angegeben werden.)

Ausgehend von Whartons Bild kann eine invariante gemeinsame Wahrscheinlichkeitsverteilung konstruiert werden, die mit jedem möglichen Paar von Anfangs- und Endbedingungen verbunden ist, und die üblichen bedingten Wahrscheinlichkeiten können durch Konditionierung auf einen beliebigen ausgewählten Teil der Grenze gebildet werden (Wharton 2010a,b). Die Wahrscheinlichkeit ist dann eine Manifestation unserer Unwissenheit: Wenn man nur die Anfangsgrenze kennen würde, könnte man das nachfolgende Feld nur probabilistisch beschreiben (aufgrund der zukünftigen Einschränkung); wenn man auch die Endgrenze kennt, könnte man die Feldwerte zwischen den beiden Grenzen retrodiktieren. (Siehe Evans, Gryb und Thébault 2016 für einen Vorschlag zur Erweiterung dieses Schemas auf den kosmologischen Kontext.)

In einer neueren Arbeit (Wharton 2016) untersucht Wharton die Aussichten für eine realistische retrokausale Interpretation der Quantentheorie auf der Grundlage des Feynman-Pfadintegral-Formalismus (Feynman 1942). In diesem Formalismus, angewandt auf ein einzelnes Teilchen, das Positionsmessungen an Raumzeitpunkten (x₀,t₀) und (x₁,t₁) unterzogen wird, wird die gemeinsame Wahrscheinlichkeitsverteilung für alle Punktepaare und die gegebenen Zeiten t₀ und t₁ beschrieben durch (Gleichung 5):

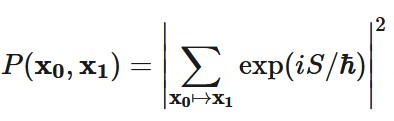
Die Summe in dieser Formel ist als infinitesimale Grenze einer diskretisierten Menge von Raumzeittrajektorien zu verstehen, die (x₀,t₀) und (x₁,t₁) verbinden. S ist die klassische Wirkung des Teilchens entlang der jeweiligen Trajektorie.

Eine einfache, aber naive Interpretation dieser Gleichung, nach der die Wahrscheinlichkeit die Unkenntnis über den eingeschlagenen Weg widerspiegelt, funktioniert nicht, da die rechte Seite von Gl. (5) nicht die Summe positiver Zahlen (interpretierbar als Wahrscheinlichkeiten von Trajektorien) ist, sondern eine positive Zahl, die durch die Bildung des Quadrats des Modulus einer Summe komplexer Zahlen erhalten wird. Wharton untersucht die Möglichkeiten, eine Interpretation des Pfadintegrals als Unwissenheit auf weniger geradlinigen Wegen zu geben, und stellt fest, dass Gleichung (5) in die folgende Form gebracht werden kann (Gleichung 6):

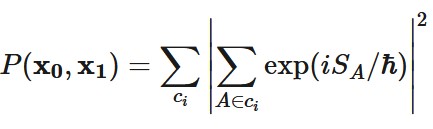
wobei die |c_i| verschiedene Gruppen von Trajektorien A sind. Die Form von Gl. (6) lädt laut Wharton zu einer Interpretation der Wahrscheinlichkeit im Hinblick auf die Unkenntnis der tatsächlichen Gruppe von Trajektorien c_i ein, und er schlägt versuchsweise eine Feldinterpretation der c_i vor. Die Interpretation ist rückwirkend, da die Wahrscheinlichkeiten über Gruppen von Trajektorien durch den zukünftigen Messzeitpunkt und die Einstellung beeinflusst werden. Offene Fragen für diesen Ansatz betreffen die Gruppierung von Trajektorien, die bisher von Natur aus mehrdeutig ist, die Details der vorgeschlagenen Feldinterpretation sowie Verallgemeinerungen auf Vielteilchen- und andere allgemeinere Einstellungen.

6.7 Die Q-basierte Interpretation

Die Husimi-Q-Funktion (Husimi 1940) ist eine nicht-negative Verteilungsfunktion im Phasenraum mit einer breiten Anwendbarkeit, z. B. in der Quantenoptik. Sie wird aus der bekannteren Wigner-Funktion (Wigner 1932) durch Glättung mit einem Gauß-Filter gewonnen. Die Q-basierte Interpretation (Drumond und Reid 2020; Friederich 2021) geht davon aus, dass jedes Quantensystem einen präzisen Phasenraumort hat und dass die Phasenraumorte gemäß der Q-Funktion verteilt sind. Infolgedessen haben alle dynamischen Variablen aller Quantensysteme in dieser Interpretation bestimmte Werte und das Messproblem wird vermieden.

Drummond und Reid (2020) argumentieren, dass diese Interpretation die in § 3 diskutierten No-Go-Theoreme über die Retrokausalitätslücke vermeidet. Zur Untermauerung dieser Behauptung verweisen sie auf ein Ergebnis von Drummond (2021), wonach sich die Q-Funktion für eine große Klasse von Quantenfeldtheorien für die Hälfte aller Freiheitsgrade über Diffusion rückwärts in der Zeit (und für die andere Hälfte vorwärts) entwickelt. Friederich (2021) schlägt vor, dass das Versagen der zeitlichen Lokalität, unabhängig motiviert durch Adlam (2018, 2022), diese Theoreme auch für die Q-basierte Interpretation ungültig machen könnte.

Es ist nicht unmittelbar offensichtlich, dass die Q-basierte Interpretation empirisch angemessen ist, da sie die aus der Born’schen Regel abgeleiteten Quantenwahrscheinlichkeiten nicht exakt reproduziert. Wie jedoch von Drummond und Reid (2020) argumentiert, ist die Diskrepanz zur Standard-Quantenmechanik, die auf der Born’schen Regel basiert, bei verschiedenen Messaufbauten und auf der Ebene makroskopischer Messgeräte möglicherweise nicht nachweisbar. Friederich (2021) liefert ein allgemeines Argument dafür, dass die Q-basierte Interpretation auf der Ebene der Messgeräte praktisch nicht von der Standard-Quantenmechanik zu unterscheiden ist, was dem Standardargument für die empirische Angemessenheit der Bohm’schen Mechanik entspricht, wie im Eintrag zur Bohm’schen Mechanik, §10, skizziert. Interessanterweise wurde eine Version der Bohm’schen Mechanik, die auch die Husimi-Funktion als tatsächliche Phasenraum-Wahrscheinlichkeitsverteilung behandelt, bereits früher von de Polavieja (1996) vorgeschlagen.

7. Einwände gegen die Retrokausalität in der Quantenmechanik

In diesem letzten Abschnitt werden einige der häufigsten und dann zwei der wichtigsten Einwände gegen den Vorschlag der Retrokausalität in der Quantenmechanik besprochen.

7.1 Allgemeine Argumente gegen die Retrokausalität

In der Philosophie gibt es die Tradition, die Idee der Retrokausalität als inkohärent zu betrachten. Die größte Sorge (Flew 1954, Black 1956) ist das sogenannte „Bilking-Argument“ (siehe den Eintrag zu Zeitreisen). Stellen Sie sich ein Ereignispaar vor, eine Ursache, C, und eine Wirkung, E, von denen wir glauben, dass sie retrokausal miteinander verbunden sind (E tritt früher in der Zeit auf als C). Es scheint möglich zu sein, ein Experiment zu entwickeln, das bestätigen könnte, ob unser Glaube an die retrokausale Verbindung richtig ist oder nicht. Wir könnten uns nämlich – sobald wir beobachtet haben, dass E eingetreten ist – daran machen, sicherzustellen, dass C nicht eintritt, wodurch jede retrokausale Verbindung, die zwischen ihnen hätte bestehen können, unterbrochen würde. Wenn wir dies erfolgreich tun würden, wäre die Wirkung ihrer Ursache „entzogen“ worden.

Das Bilking-Argument führt zu der Behauptung, dass jede Überzeugung, die ein Akteur von der positiven retrokausalen Korrelation zwischen Ereignis C und Ereignis E haben könnte, einfach falsch ist. Dummett (1964) bestreitet jedoch, dass die einzige Lösung für das Bilking-Argument darin besteht, diesen Glauben aufzugeben. Dummett zufolge zeigt das Bilking-Argument vielmehr, dass eine Reihe von drei Bedingungen, die die beiden Ereignisse und die Beziehung des Agenten zu ihnen betreffen, inkohärent sind:

i. Es besteht eine positive Korrelation zwischen einem Ereignis C und einem Ereignis E.

ii. Es liegt in der Macht eines Agenten, C auszuführen.

iii. Der Agent hat erkenntnistheoretischen Zugang zum Eintreten von Ereignis E, unabhängig von der Absicht, es herbeizuführen.

Es ist interessant festzustellen, dass diese Bedingungen nicht angeben, in welcher Reihenfolge die Ereignisse C und E eintreten. Bei einfacher Überlegung gibt es einen ganz natürlichen Grund, warum es nicht möglich ist, zukünftige Auswirkungen ihrer Ursachen zu berauben, da Bedingung (iii) für zukünftige Ereignisse nicht gilt: Wir haben einfach keinen Zugang zu den zukünftigen Ereignissen, die unabhängig von der Rolle eintreten, die wir als kausale Agenten spielen, um die Ereignisse herbeizuführen. Wenn uns dieser erkenntnistheoretische Zugang zu vergangenen Ereignissen fehlt, steht uns derselbe Ausweg aus dem Bilking-Argument zur Verfügung.

Dummetts Verteidigung gegen das Bilking-Argument ist besonders relevant für die Quantenmechanik. Sobald eine geeignete Spezifikation darüber vorliegt, wie Bedingung (iii) verletzt werden kann, stellen wir fest, dass es eine starke Parallele zwischen den Bedingungen, die erfüllt sein müssen, um den Glauben an die Beeinflussung der Vergangenheit zu rechtfertigen, und der Struktur der Quantenmechanik gibt. Price (1996: 174) weist darauf hin, dass Betrug unter den folgenden Umständen unmöglich ist: Anstatt anzunehmen, dass eine Verletzung der Bedingung (iii) dazu führt, dass der betreffende Akteur keinen erkenntnistheoretischen Zugang zu den relevanten vergangenen Ereignissen hat, unabhängig von der Absicht, sie herbeizuführen, sollte man annehmen, dass die Mittel, mit denen das Wissen über diese vergangenen Ereignisse gesammelt wird, die behauptete Korrelation zwischen der Handlung des Akteurs und diesen vergangenen Ereignissen aufheben. Eine solche Bedingung kann wie folgt formuliert werden:

iv. Der Akteur kann unabhängig von der Absicht, das Ereignis herbeizuführen, und ohne das Ereignis E gegenüber dem zu verändern, was es gewesen wäre, wenn kein erkenntnisbasierter Zugang erlangt worden wäre, erkenntnisbasierten Zugang zum Eintreten des Ereignisses E erlangen.

Die Bedeutung dieser abgeschwächten Verletzung der Bedingung (iii) ist, dass es genau die Art von Bedingung ist, die man erwarten würde, wenn das fragliche System ein Quantensystem wäre. Die Natur der Quantenmechanik stellt sicher, dass jede behauptete positive Korrelation zwischen den zukünftigen Messeinstellungen und den verborgenen Variablen, die ein Quantensystem charakterisieren, unmöglich von ihren Ursachen losgelöst werden kann, da Bedingung (iv) ständig verletzt wird. Darüber hinaus fehlt uns, solange wir uns der erkenntnistheoretischen Interpretation der Wellenfunktion anschließen, der erkenntnistheoretische Zugang zu den „verborgenen“ Variablen des Systems, und dieser Zugang fehlt uns im Prinzip aufgrund der Struktur der Quantentheorie.

Eine weitere bekannte Herausforderung für die Idee der Retrokausalität besteht darin, dass sie unweigerlich zu Teufelskreisen führen würde (Mellor 1998). (Siehe Faye 1994 für eine Antwort und den Eintrag zu rückwärts gerichteter Kausalität für eine detailliertere Übersicht über die Einwände gegen die Idee der Rückkausalität.)

7.2 Retrokausalität ist einfach Superdeterminismus

Erinnern wir uns (§3.1) daran, dass Retrokausalität als explizite Verletzung der Annahme der Messunabhängigkeit (Gl. (1)) als Mittel zur Umgehung des Bell’schen Theorems motiviert werden kann. Es gibt jedoch einen weiteren möglichen Mechanismus, der Verstöße gegen die Messunabhängigkeit untermauern könnte, nämlich den Superdeterminismus. Dies ist die Idee, dass in der Terminologie von §3 die gemeinsame Vergangenheit von (i) der Messeinstellung α und (ii) dem verborgenen Zustand des gemessenen Systems λ beide vollständig bestimmt und die relevanten Quanten-Korrelationen zwischen ihnen induziert (siehe den Eintrag zu Bell’s Theorem, §8.1.1, und die darin enthaltenen Verweise). Hossenfelder (2020) argumentiert dagegen, Verstöße gegen die Messunabhängigkeit als „Retrokausalität“ zu bezeichnen, und zieht es vor, solche Verstöße ausschließlich als Fälle von „Superdeterminismus“ zu betrachten, da „die Idee einer Ursache, die sich in der Zeit zurück ausbreitet, bedeutungslos ist“ (2020:10; siehe auch Hossenfelder und Palmer (2020)). Der wesentliche Streitpunkt hierbei ist, und darauf weist Hossenfelder ausdrücklich hin, dass sowohl die Retrokausalität als auch der Superdeterminismus ein unterschiedliches Verständnis der Natur der Kausalität voraussetzen.

Die Charakterisierung von Kausalität, die Hossenfelder (2020: 10) verwendet, um den Vorschlag der Retrokausalität zu untergraben, besagt, dass A eine Ursache für B ist, wenn und nur wenn A und B korreliert sind und B sich im Vorwärtslichtkegel von A befindet: „Wenn Sie glauben, dass Sie eine Situation haben, in der B A ‚retrokausal‘ verursacht, dann bedeutet dies lediglich, dass A B verursacht“. Auf diese Weise sollten solche Korrelationen zwischen Ereignissen niemals als retrokausal verstanden werden, sondern immer als superdeterministisch. Diese Charakterisierung der Kausalität erinnert an Humes Konventionalismus in Bezug auf Ursache und Wirkung, wonach es lediglich eine Frage der Terminologie ist, dass Ursachen ihren Wirkungen vorausgehen müssen (siehe den Eintrag zu Retrokausalität, §2.3). Wie in den metaphysischen Vorbemerkungen in §2.1 erwähnt, ist das Konzept der Kausalität, das am ehesten mit dem Vorschlag der Retrokausalität übereinstimmt, ein interventionistisches. Hossenfelder erkennt dies an und argumentiert, dass der Grund, warum die interventionistische Darstellung der Kausalität als Vorschlag im Quantenkontext ungeeignet ist, darin besteht, dass „Agenten“ und ihre „Interventionen“ makroskopische Begriffe sind, die in der Quantenmechanik nicht vorkommen.

Hossenfelders Kritik betont, dass die Retrokausalität ein bestimmtes Paket metaphysischer Ansichten erfordert, um ein tragfähiger Vorschlag zu sein. Hossenfelders Analyse stützt sich auf ein Kausalitätskonzept, das im Widerspruch zum interventionistischen Ansatz steht, insbesondere wenn man es, wie in §2.1 dargelegt, entlang perspektivischer Linien betrachtet. Daher müsste eine Verteidigung der Retrokausalität gegen Hossenfelders Einwand die Fruchtbarkeit dieser Darstellung der Kausalität verteidigen.

7.3 Retrokausalität erfordert Feinabstimmung

Die Kausalmodellierung (Spirtes, Glymour, & Scheines 2000; Pearl 2009) ist eine Praxis, die aus dem Bereich des maschinellen Lernens hervorgegangen ist und in der Entwicklung von Algorithmen besteht, die die Entdeckung von Ursachen aus Korrelationen in großen Datensätzen automatisieren können. Die Algorithmen zur Kausalerforschung ermöglichen eine Ableitung von gegebenen statistischen Abhängigkeiten und Unabhängigkeiten zwischen verschiedenen messbaren Elementen eines Systems zu einem Kausalmodell für dieses System. Als Teil der Algorithmen muss eine Reihe von Einschränkungen auf die resultierenden Modelle angewendet werden, die allgemeine Merkmale erfassen, die wir als charakteristisch für Kausalität betrachten. Zwei der wichtigsten Annahmen sind (i) die kausale Markov-Bedingung, die sicherstellt, dass jede statistische Abhängigkeit in den Daten zu einer kausalen Abhängigkeit im Modell führt – im Wesentlichen eine Formalisierung des Prinzips der gemeinsamen Ursache von Reichenbach – und (ii) die Treue, die sicherstellt, dass jede statistische Unabhängigkeit eine kausale Unabhängigkeit impliziert oder dass keine kausale Unabhängigkeit das Ergebnis einer Feinabstimmung des Modells ist.

Es ist seit langem bekannt (Butterfield 1992; Hausman 1999; Hausman & Woodward 1999), dass Quantenkorrelationen dazu zwingen, mindestens eine der Annahmen aufzugeben, die normalerweise im Rahmen der Kausalmodellierung getroffen werden. Wood und Spekkens (2015) argumentieren, dass jedes Kausalmodell, das vorgibt, die beobachteten Quanten-Korrelationen kausal zu erklären, fein abgestimmt werden muss (d. h. die Treueannahme verletzen muss). Genauer gesagt, da die beobachteten statistischen Unabhängigkeiten in einem verschränkten, bipartiten Quantensystem keine Signalisierung zwischen den Parteien implizieren, muss, wenn dann angenommen wird, dass jede statistische Unabhängigkeit eine kausale Unabhängigkeit impliziert (was die Treue vorschreibt), daraus geschlossen werden, dass es keine (direkte oder vermittelte) kausale Verbindung zwischen den Parteien geben kann. Da eine beobachtete statistische Abhängigkeit zwischen den Ergebnissen von Messungen am bipartiten System besteht, können wir diese Abhängigkeit nicht mehr mit einem Kausalzusammenhang erklären, es sei denn, dieser Zusammenhang ist so fein abgestimmt, dass die Unabhängigkeit ohne Signalisierung weiterhin gewährleistet ist. Es besteht somit eine grundlegende Spannung zwischen den beobachteten Quantenkorrelationen und der Anforderung der Unabhängigkeit ohne Signalisierung, der Treueannahme und der Möglichkeit einer kausalen Erklärung.

Formal argumentieren Wood und Spekkens, dass die folgenden drei Annahmen einen inkonsistenten Satz bilden: (i) die Vorhersagen der Quantentheorie bezüglich der beobachteten statistischen Abhängigkeiten und Unabhängigkeiten sind korrekt; (ii) die beobachteten statistischen Abhängigkeiten und Unabhängigkeiten können kausal erklärt werden; (iii) die Treueannahme gilt. Wood und Spekkens kommen zu dem Schluss, dass die zweite Annahme nachgeben muss, da die Treueannahme ein unverzichtbares Element der Kausalitätsentdeckung ist. Das Gegenteil davon ist, dass jede angebliche kausale Erklärung der beobachteten Korrelationen in einem verschränkten, bipartiten Quantensystem mit dem Konflikt zwischen der Nicht-Signalübertragung und der Nicht-Feinabstimmung in Konflikt gerät und daher die Treueannahme verletzen muss. Solche kausalen Erklärungen, so das Argument, einschließlich rückwirkender Erklärungen, sollten daher als brauchbare Erklärungen ausgeschlossen werden.

Als kurze Anmerkung: Diese Sorge um die Feinabstimmung der Rückkopplung im Quantenkontext stellt sich auf direktere Weise. Es gibt keine guten Belege dafür, dass eine Signalübertragung in die Vergangenheit möglich ist; das heißt, es gibt keine Rückkopplung auf der operativen Ebene. (Pegg 2006, 2008 argumentiert, dass dies formal als Ergebnis der Vollständigkeitsbestimmung der Messoperatoren erklärt werden kann, wodurch eine Asymmetrie in den Normalisierungsbedingungen für Vorbereitung und Messung eingeführt wird.) Doch obwohl es keine Signalisierung in die Vergangenheit gibt, gehen retrokausale Darstellungen von kausalen Einflüssen in die Vergangenheit aus. Dass diese kausalen Einflüsse nicht als statistische Abhängigkeiten auftreten, die für Signalisierungszwecke genutzt werden können, wirft genau die gleichen Bedenken hinsichtlich der Feinabstimmung auf, die Wood und Spekkens äußern.

Eine offensichtliche Antwort auf die von Wood und Spekkens gestellte Herausforderung besteht darin, die Annahme der Treue einfach abzulehnen. Dies sollte jedoch nicht auf die leichte Schulter genommen werden, da die Intuition hinter der Treueannahme grundlegend und überzeugend ist. Wenn zwischen dem Auftreten eines Ereignispaares keine statistische Korrelation besteht, gibt es keinen Grund für die Annahme, dass zwischen ihnen ein kausaler Zusammenhang besteht. Umgekehrt wäre es eine besonders schwierige Aufgabe, festzustellen, welche dieser unkorrelierten Mengen einen konspirativen kausalen Zusammenhang bergen könnte, der die Korrelation verbirgt, wenn wir die Möglichkeit eines kausalen Zusammenhangs zwischen statistisch unkorrelierten Ereignissen zulassen würden. Die Treueannahme ist somit ein Prinzip der Sparsamkeit – die einfachste Erklärung für ein Paar statistisch unkorrelierter Ereignisse ist, dass sie kausal unabhängig sind – ähnlich wie Spekkens‘ (2005) Definition von Kontextualität (siehe §3.2); tatsächlich argumentiert Cavalcanti (2018), dass Kontextualität als eine Form der Feinabstimmung ausgelegt werden kann.

Es gibt jedoch bekannte Beispiele für Systeme, die möglicherweise eine falsche Anwendung der Treueannahme aufweisen. Ein solches Beispiel, das auf Hesslow (1976) zurückgeht, betrifft eine Antibabypille, die Thrombosen verursachen kann, während sie gleichzeitig die Wahrscheinlichkeit einer Schwangerschaft senkt, die ebenfalls Thrombosen verursachen kann. Wie Cartwright (2001: 246) betont, ist es bei einem angemessenen Gewicht dieser Prozesse denkbar, dass der Nettoeffekt der Pillen auf die Häufigkeit von Thrombosen gleich Null ist. Dies ist ein Fall von „aufhebenden Pfaden“, bei dem sich die Wirkung von zwei oder mehr Kausalpfaden zwischen einem Variablenpaar aufhebt, um statistische Unabhängigkeit zu erreichen. In einem Fall wie diesem, in dem wir über die einzelnen beteiligten Kausalmechanismen unabhängige Kenntnisse haben können, gibt es Gründe für die Annahme, dass es trotz ihrer statistischen Unabhängigkeit tatsächlich einen Kausalzusammenhang zwischen den Variablen gibt. Es ist also durchaus möglich, sich ein Szenario vorzustellen, in dem die Treueannahme in die Irre führen könnte. Zur Verteidigung des allgemeinen Prinzips enthält ein Beispiel wie dieses jedoch eindeutig das, was Wood und Spekkens als Feinabstimmung bezeichnen; die spezifischen Gewichte für diese Prozesse müssten genau übereinstimmen, um die statistische Abhängigkeit zu beseitigen, und ein solches Gleichgewicht würde im Allgemeinen als instabil angesehen werden (jede Änderung der Hintergrundbedingungen usw. würde den Kausalzusammenhang in Form einer statistischen Abhängigkeit aufdecken).

Näger (2016) weist darauf hin, dass Untreue auch ohne konspirative Feinabstimmung auftreten kann, wenn sie auf stabile Weise entsteht. Im Zusammenhang mit der Quantenphysik schlägt Näger vor, dass der Feinabstimmungsmechanismus das ist, was er „interne Aufhebungswege“ nennt. Dieser Mechanismus ist analog zum üblichen Szenario der Aufhebungswege, aber der Wegaufhebungsmechanismus manifestiert sich nicht auf der Ebene der Variablen, sondern auf der Ebene der Werte. Aus dieser Sicht würde eine solche Feinabstimmung als Ergebnis des bestimmten kausalen und/oder nomologischen Prozesses erfolgen, der das System steuert, und in diesem Sinne ist der Mechanismus der aufhebenden Pfade intern, und es ist die Tatsache, dass der Mechanismus intern ist, die die damit verbundene Feinabstimmung gegenüber externen Störungen stabil macht.

Wenn die Naturgesetze so beschaffen sind, dass Störungen die verschiedenen Pfade immer auf ausgewogene Weise verändern, dann ist es physikalisch unmöglich, die Pfade aus dem Gleichgewicht zu bringen. (Näger 2016: 26)

Die von Näger aufgeworfene Möglichkeit würde das Problem umgehen, dass Verletzungen der Treue letztlich unsere Fähigkeit untergraben, angemessene Rückschlüsse auf die kausale Unabhängigkeit auf der Grundlage der statistischen Unabhängigkeit zu ziehen, indem nur eine bestimmte Art von Untreue zugelassen wird – eine prinzipien- oder gesetzesbasierte Untreue, die „intern“ und somit stabil gegenüber Hintergrundbedingungen ist –, was viel weniger „verschwörerisch“ ist, da die Feinabstimmung eine Funktion des spezifischen Prozesses ist. Evans (2018) argumentiert, dass ein grundlegendes retrokausales Modell der Art, wie es von Costa de Beauregard (siehe §1) ins Auge gefasst wurde, genau eine solche Erklärung interner aufhebender Pfade verwendet, um die untreuen (nicht signalisierenden) Kausalkanäle zu erklären. Siehe auch Almada et al. (2016) für ein Argument, dass die Feinabstimmung im Quantenkontext robust sei und sich aus Symmetrieüberlegungen ergibt. Darüber hinaus argumentiert Evans (2021), dass Fälle von Feinabstimmung gemäß der Analyse von Wood und Spekkens allgegenwärtiger sein könnten, als wir vermuten, und wir uns daher nicht so viele Sorgen über solche Quantenfälle machen sollten.

7.4 Kontextualität für exotische Kausalstrukturen

Erinnern Sie sich (§3.2) daran, dass Spekkens‘ (2005) Behauptung, dass kein nichtkontextuelles ontologisches Modell die beobachteten Statistiken der Quantentheorie reproduzieren könnne – basierend auf seinem Prinzip der Sparsamkeit (dass es keinen ontologischen Unterschied ohne operationellen Unterschied gibt) -durch retrokausale Ansätze umgangen wurde, da der ontologische Modellrahmen ausdrücklich davon ausgeht, dass der ontische Zustand unabhängig vom Messverfahren ist (d. h. dass es keine Retrokausalität gibt). Es wurde dort die Möglichkeit erwähnt, dass Spekkens‘ Prinzip der Sparsamkeit neu formuliert werden könnte, um allgemeiner auf retrokausale Modelle angewendet zu werden. Shrapnel und Costa (2018) erreichen genau dies in einem No-Go-Theorem, das auf jede exotische Kausalstruktur anwendbar ist, die zur Umgehung des ontologischen Modellrahmens verwendet wird, einschließlich retrokausaler Darstellungen, wodurch solche Modelle letztlich kontextabhängig werden.

Das Ergebnis von Shrapnel und Costa basiert auf einer Verallgemeinerung des ontologischen Modellrahmens, der die operativen Vorbereitungs-, Transformations- und Messverfahren durch die zeitlich und kausal neutralen Begriffe der lokalen Kontrollierbarkeit und der Umweltprozesse ersetzt, die Korrelationen zwischen verschiedenen lokalen Systemen vermitteln und die gemeinsame Statistik für eine Reihe von Ereignissen generieren. „Dazu gehören alle globalen Eigenschaften, Anfangszustände, Verbindungsmechanismen, kausalen Einflüsse oder globale Dynamiken“ (2018: 5). Darüber hinaus ersetzen sie den ontischen Zustand λ durch den ontischen „Prozess“ ω:

Unser ontischer Prozess erfasst die physischen Eigenschaften der Welt, die unter unseren lokalen Operationen unveränderlich bleiben. Das heißt, obwohl wir zulassen, dass sich lokale Eigenschaften unter bestimmten Operationen verändern, möchten wir, dass unser ontischer Prozess die Aspekte der Realität erfasst, die unabhängig von dieser Sondierung sind. (2018: 8)

Daher wird der Begriff der λ-Mediation (der in §4.1 behandelt wird) durch den Begriff der ω-Mediation ersetzt, bei dem der ontische Prozess ω die Eigenschaften der Umgebung, die Korrelationen zwischen Regionen vermitteln, vollständig spezifiziert und die von lokalen Kontrollvariablen erzeugten Ergebnisse vom Rest der Umgebung abschirmt. Shrapnel und Costa (2018: 9) definieren den Begriff der „Instrumenten-Nichtkontextualität“ als ein Gesetz der Sparsamkeit (in Anlehnung an Spekkens‘ eigene Definition von Nichtkontextualität): „Operativ nicht unterscheidbare Paare von Ergebnissen und lokalen Kontrollgrößen sollten auf ontologischer Ebene nicht unterscheidbar bleiben“. Sie zeigen dann, dass kein Instrumenten-Nichtkontextmodell die quantenstatistischen Vorhersagen reproduzieren kann.

Entscheidend ist, dass nicht nur die traditionelle Vorstellung von „Zustand“ kontextabhängig ist, sondern auch jedes vermeintlich objektive Merkmal der Theorie, wie z. B. ein dynamisches Gesetz oder eine Randbedingung. (2018: 2)

Da Vorbereitungen, Transformationen und Messungen durch lokale Kontrollgrößen ersetzt wurden, gibt es in Shrapnels und Costas Rahmen keine zusätzliche Annahme, dass ω mit einigen Kontrollvariablen korreliert, aber von anderen unabhängig ist. Somit ist der übliche Weg aus dem ontologischen Modellrahmen und damit die No-Go-Theoreme von §3, die für retrokausale Ansätze offen sind – der Rahmen geht von keiner Retrokausalität aus –, im Shrapnel-Costa-Theorem verschlossen, wodurch retrokausale Ansätze zusammen mit den übrigen Modellen, die vom ontologischen Modellrahmen erfasst werden, kontextabhängig werden.

Dies stellt eine erhebliche Sorge für retrokausale Ansätze in der Quantentheorie dar. Wenn die Hauptmotivation für die Verfolgung der Hypothese der Retrokausalität darin besteht, in gewisser Weise eine klassische Ontologie für die Quantentheorie wiederherzustellen (siehe §3.4), dann hat der Shrapnel-Costa-Satz diese Aufgabe entweder unmöglich gemacht oder von der Möglichkeit einer weiteren Geschichte abhängig gemacht, die erklärt, wie die kontextuellen Merkmale des Modells aus einer nichtkontextuellen Grundlage entstehen. Was den letztgenannten Punkt betrifft, ist es schwierig zu erkennen, wie diese Geschichte erzählt werden könnte, ohne die ideologische Ökonomie des konzeptuellen Rahmens der Retrokausalität erheblich zu reduzieren, was wiederum eine potenzielle Tugend der Retrokausalität gefährden würde (siehe Evans 2020 für eine weitere Diskussion dieses Punktes).

Wie oben erwähnt (§7.3), kann Kontextualität als eine Form der Feinabstimmung ausgelegt werden (Cavalcanti 2018; Adlam 2021), insbesondere wenn die Forderung nach Nichtkontextualität als eine Anforderung der Sparsamkeit verstanden wird, wie oben. Die in diesem und im letzten Abschnitt geäußerten Bedenken unterstreichen die Tatsache, dass die Herausforderung, verschiedene Arten der Feinabstimmung zu berücksichtigen, das schwerwiegendste prinzipielle Hindernis darstellt, mit dem retrokausale Erklärungen weiterhin konfrontiert sind.

Bibliographie

Adlam, Emily, 2018, “Spooky Action at a Temporal Distance”, Entropy, 20: 41. doi:10.3390/e20010041
–––, 2021, “Contextuality, Fine-Tuning and Teleological Explanation”, Foundations of Physics, 51: 106. doi:10.1007/s10701-021-00516-y
–––, 2022, “Two roads to retrocausality”, Synthese, 200: 422. doi:10.1007/s11229-022-03919-0

Aharonov, Yakir, Peter G. Bergmann, and Joel L. Lebowitz, 1964, “Time Symmetry in the Quantum Process of Measurement”, Physical Review, 134(6B): B1410–B1416. doi:10.1103/PhysRev.134.B1410

Aharonov, Yakir and Lev Vaidman, 1991, “Complete Description of a Quantum System at a given Time”, Journal of Physics A: Mathematical and General, 24(10): 2315–2328. doi:10.1088/0305-4470/24/10/018
–––, 2007, “The Two-State Vector Formalism: An Updated Review”, in Time in Quantum Mechanics, J.G. Muga, R. Sala

Mayato, and Í.L. Egusquiza (eds.), (Lecture Notes in Physics 734), Berlin, Heidelberg: Springer Berlin Heidelberg, 399–447. doi:10.1007/978-3-540-73473-4_13

Allen, John-Mark A., Jonathan Barrett, Dominic C. Horsman, Ciarán M. Lee, and Robert W. Spekkens, 2017, “Quantum Common Causes and Quantum Causal Models”, Physical Review X, 7(3): 031021. doi:10.1103/PhysRevX.7.031021

Almada, D., K. Ch’ng, S. Kintner, S., B. Morrison, and Ken B. Wharton, 2016, “Are Retrocausal Accounts of Entanglement Unnaturally Fine-tuned?”, International Journal of Quantum Foundations, 2(1): 1–16. [Almada et al. 2016 available online]

Argaman, Nathan, 2010, “Bell’s Theorem and the Causal Arrow of Time”, American Journal of Physics, 78(10): 1007–1013. doi:10.1119/1.3456564

Aspect, Alain, Jean Dalibard, and Gérard Roger, 1982, “Experimental Test of Bell’s Inequalities Using Time- Varying Analyzers”, Physical Review Letters, 49(25): 1804–1807. doi:10.1103/PhysRevLett.49.1804

Aspect, Alain, Philippe Grangier, and Gérard Roger, 1982, “Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment : A New Violation of Bell’s Inequalities”, Physical Review Letters, 49(2): 91–94. doi:10.1103/PhysRevLett.49.91

Atkinson, D., 2000, “Quantum Mechanics and Retrocausality”, in Naresh Dadhich, and Ajit Kembhavi (eds.), The Universe, Visions and Perspectives, Dordrecht: Kluwer Academic Publishers, pp. 35–50.

Becker, Adam, 2018, “Quantum Time Machine: How the Future Can Change What Happens Now”, New Scientist, 14 February 2018.

Bell, John S., 1964, “On the Einstein Podolsky Rosen Paradox”, Physics Physique Fizika, 1(3): 195–200. Reprinted in Bell 2004 14–21. doi:10.1103/PhysicsPhysiqueFizika.1.195
–––, 1966, “On the Problem of Hidden Variables in Quantum Mechanics”, Reviews of Modern Physics, 38(3): 447–452. Reprinted in Bell 2004, pp. 1–13. doi:10.1103/RevModPhys.38.447
–––, 1976, “The Theory of Local Beables”, Epistemological Letters, 9: 11–24. Reprinted in Bell 2004: 52–62. [Bell 1976available online]
–––, 1990, “La Nouvelle Cuisine”, in A. Sarlemijn, and P. Kroes (eds.), Between Science and Technology, Amsterdam: Elsevier, pp. 97–115. Reprinted in Bell 2004: 232–248.
–––, 2004, Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy, second edition, Cambridge: Cambridge University Press. doi:10.1017/CBO9780511815676

Berkovitz, Joseph, 2002, “On Causal Loops in the Quantum Realm”, in Non-Locality and Modality, Tomasz Placek and Jeremy Butterfield (eds.), Dordrecht: Springer Netherlands, 235–257. doi:10.1007/978-94-010-0385-8_16
–––, 2008, “On Predictions in Retro-Causal Interpretations of Quantum Mechanics”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 39(4): 709–735. doi:10.1016/j.shpsb.2008.08.002

Black, M., 1956, “Why Cannot an Effect Precede Its Cause?”, Analysis, 16(3): 49–58. doi:10.1093/analys/16.3.49

Bohm, David, 1952a, “A Suggested Interpretation of the Quantum Theory in Terms of ‘Hidden’ Variables. I”, Physical Review, 85(2): 166–179. doi:10.1103/PhysRev.85.166
–––, 1952b, “A Suggested Interpretation of the Quantum Theory in Terms of ‘Hidden’ Variables. II”, Physical Review, 85(2): 180–193. doi:10.1103/PhysRev.85.180

Brunner, Nicolas, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner, 2014, “Bell Nonlocality”, Reviews of Modern Physics, 86(2): 419–478. doi:10.1103/RevModPhys.86.419

Butterfield, Jeremy, 1992, “Bell’s Theorem: What It Takes”, The British Journal for the Philosophy of Science, 43(1): 41–83. doi:10.1093/bjps/43.1.41

Cartwright, Nancy, 1979, “Causal Laws and Effective Strategies”, Noûs, 13(4): 419. doi:10.2307/2215337
–––, 2001, “What Is Wrong With Bayes Nets?”:, Monist, 84(2): 242–264. doi:10.5840/monist20018429

Cavalcanti, Eric G., 2018, “Classical Causal Models for Bell and Kochen-Specker Inequality Violations Require Fine-Tuning”, Physical Review X, 8(2): 021018. doi:10.1103/PhysRevX.8.021018

Cavalcanti, Eric G and Raymond Lal, 2014, “On Modifications of Reichenbachʼs Principle of Common Cause in Light of Bellʼs Theorem”, Journal of Physics A: Mathematical and Theoretical, 47(42): 424018. doi:10.1088/1751-8113/47/42/424018

Clauser, John F., Michael A. Horne, Abner Shimony, and Richard A. Holt, 1969, “Proposed Experiment to Test Local Hidden-Variable Theories”, Physical Review Letters, 23(15): 880–884. doi:10.1103/PhysRevLett.23.880

Colbeck, Roger and Renato Renner, 2012, “Is a System’s Wave Function in One-to-One Correspondence with Its Elements of Reality?”, Physical Review Letters, 108(15): 150402. doi:10.1103/PhysRevLett.108.150402

Corry, Richard, 2015, “Retrocausal Models for EPR”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 49: 1–9. doi:10.1016/j.shpsb.2014.11.001

Costa, Fabio, and Shrapnel, Sally, 2016, “Quantum Causal Modelling”, New Journal of Physics, 18: 063032. doi:10.1088/1367-2630/18/6/063032

Costa de Beauregard, Olivier, 1953, “Mécanique Quantique”, Comptes Rendus Académie des Sciences, 236: 1632–1634. [Costa de Beauregard 1953 available online]
–––, 1976, “Time Symmetry and Interpretation of Quantum Mechanics”, Foundations of Physics, 6(5): 539–559. doi:10.1007/BF00715107
–––, 1977a, “Les duellistes Bell et Clauser-Horne-Shimony (<>) s’aveuglent en refusant la <> inscrite en clair dans le formalisme”, Epistemological Letters, 16: 1–8.
–––, 1977b, “Time Symmetry and the Einstein Paradox”, Il Nuovo Cimento B, 42(1): 41–64. doi:10.1007/BF02906749
–––, 1987a, “On the Zigzagging Causality EPR Model: Answer to Vigier and Coworkers and to Sutherland”, Foundations of Physics, 17(8): 775–785. doi:10.1007/BF00733266
–––, 1987b, Time, The Physical Magnitude, Dordrecht: D. Reidel.

Cramer, John G., 1980, “Generalized Absorber Theory and the Einstein-Podolsky-Rosen Paradox”, Physical Review D, 22(2): 362–376. doi:10.1103/PhysRevD.22.362
–––, 1986, “The Transactional Interpretation of Quantum Mechanics”, Reviews of Modern Physics, 58(3): 647–687. doi:10.1103/RevModPhys.58.647
–––, 1988, “An Overview of the Transactional Interpretation of Quantum Mechanics”, International Journal of Theoretical Physics, 27(2): 227–236. doi:10.1007/BF00670751
–––, 2016, The Quantum Handshake, Cham: Springer International Publishing. doi:10.1007/978-3-319-24642-0

de Polavieja, Gonzalo G., 1996, “A Causal Quantum Theory in Phase Space”, Physics Letters A, 220(6): 303–314. doi:10.1016/0375-9601(96)00523-3

Dirac, Paul Adrien Maurice, 1938, “Classical Theory of Radiating Electrons”, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 167(929): 148–169. doi:10.1098/rspa.1938.0124

Drummond, Peter, 2021, “Time Evolution with Symmetric Stochastic Action”, Physical Review Research, 3(1): 013240. doi:10.1103/PhysRevResearch.3.013240

Drummond, Peter, and Margaret Reid, 2020, “Retrocausal Model of Reality for Quantum Fields”, Physical Review Research, 2(3): 033266. doi:10.1103/PhysRevResearch.2.033266

Dummett, Michael, 1964, “Bringing About the Past”, The Philosophical Review, 73(3): 338. doi:10.2307/2183661

Einstein, Albert, 1948, “Quanten-Mechanik Und Wirklichkeit”, Dialectica, 2(3–4): 320–324. doi:10.1111/j.1746-8361.1948.tb00704.x

Einstein, Albert, Boris Podolsky, and Nathan Rosen, 1935, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”, Physical Review, 47(10): 777–780. doi:10.1103/PhysRev.47.777

Evans, Peter W., 2015, “Retrocausality at No Extra Cost”, Synthese, 192(4): 1139–1155. doi:10.1007/s11229-014-0605-0
–––, 2018, “Quantum Causal Models, Faithfulness, and Retrocausality”, The British Journal for the Philosophy of Science, 69(3): 745–774. doi:10.1093/bjps/axw037
–––, 2020, “The End of a Classical Ontology for Quantum Mechanics?”, Entropy, 23(1): 12. doi:10.3390/e23010012
–––, 2021, “A Sideways Look at Faithfulness for Quantum Correlations”, The Journal of Philosophy, 118(1): 28–42. doi:10.5840/jphil202111812

Evans, Peter W., Sean Gryb and Karim P. Y. Thébault, 2016, “Ψ-epistemic quantum cosmology?”, Studies in History and Philosophy of Modern Physics, 56: 1–12. doi:10.1016/j.shpsb.2016.10.005

Evans, Peter W., Huw Price, and Ken B. Wharton, 2013, “New Slant on the EPR-Bell Experiment”, The British Journal for the Philosophy of Science, 64(2): 297–324. doi:10.1093/bjps/axr052

Faye, Jan, 1994, “Causal Beliefs and their Justification”, in Logic and Causal Reasoning, Jan Faye, Uwe Scheffler, and Max Urchs (eds.), Berlin: Akademie Verlag, pp. 141–168.

Feynman, Richard P., 1942 [2005], “The Principle of Least Action in Quantum Mechanics”, PhD Thesis, Princeton University. Reprinted in Feynman’s Thesis: A New Approach to Quantum Theory, Laurie M. Brown (ed.), Singapore: World Scientific Publishing, 2005, pp. 1–69. [Feynman 1942 available online]

Flew, Antony, 1954, “Can an Effect Precede its Cause?”, Proceedings of the Aristotelian Society, 28(Supplement): 45–62.

Freedman, Stuart J. and John F. Clauser, 1972, “Experimental Test of Local Hidden-Variable Theories”, Physical Review Letters, 28(14): 938–941. doi:10.1103/PhysRevLett.28.938

Friederich, Simon, 2021, “Introducing the Q-based interpretation of quantum mechanics”, The British Journal for the Philosophy of Science, online first. doi:10.1086/716196

Frisch, Mathias, 2014, Causal Reasoning in Physics, Cambridge: Cambridge University Press.

Ghirardi, G. C., A. Rimini, and T. Weber, 1986, “Unified Dynamics for Microscopic and Macroscopic Systems”, Physical Review D, 34(2): 470–491. doi:10.1103/PhysRevD.34.470

Goldstein, Sheldon, Travis Norsen, Daniel Tausk, and Nino Zanghi, 2011, “Bell’s Theorem”, Scholarpedia, 6(10): 8378. doi:10.4249/scholarpedia.8378

Greenberger, Daniel M., Michael A. Horne, and Anton Zeilinger, 1989, “Going Beyond Bell’s Theorem”, in Bell’s Theorem, Quantum Theory and Conceptions of the Universe, Menas Kafatos (ed.), Dordrecht: Springer Netherlands, 69–72. doi:10.1007/978-94-017-0849-4_10

Hardy, Lucien, 2013, “Are Quantum States Real?”, International Journal of Modern Physics B, 27(01n03): 1345012. doi:10.1142/S0217979213450124

Harrigan, Nicholas and Robert W. Spekkens, 2010, “Einstein, Incompleteness, and the Epistemic View of Quantum States”, Foundations of Physics, 40(2): 125–157. doi:10.1007/s10701-009-9347-0

Hausman, Daniel M., 1999, “Lessons From Quantum Mechanics”, Synthese, 121(1/2): 79–92. doi:10.1023/A:1005281714660

Hausman, Daniel M. and James Woodward, 1999, “Independence, Invariance and the Causal Markov Condition”, The British Journal for the Philosophy of Science, 50(4): 521–583. doi:10.1093/bjps/50.4.521

Hermens, Ronnie, 2011, “The Problem of Contextuality and the Impossibility of Experimental Metaphysics Thereof”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 42(4): 214–225. doi:10.1016/j.shpsb.2011.06.001

Hesslow, Germund, 1976, “Two Notes on the Probabilistic Approach to Causality”, Philosophy of Science, 43(2): 290–292. doi:10.1086/288684

Hokkyo, Noboru, 1988, “Variational Formulation of Transactional and Related Interpretations of Quantum Mechanics”, Foundations of Physics Letters, 1(3): 293–299. doi:10.1007/BF00690070

Hossenfelder, Sabine and Tim Palmer, 2020, “Rethinking Superdeterminism”, Frontiers in Physics, 8: 139. 10.3389/fphy.2020.00139
–––, 2008, “Retrocausation Acting in the Single-Electron Double-Slit Interference Experiment”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 39(4): 762–766. doi:10.1016/j.shpsb.2008.05.001

Husimi, Kôdi, 1940, “Some Formal Properties of the Density Matrix”, Proceedings of the Physico-Mathematical Society of Japan, 22(4): 264–314.

Ismael, Jenann, 2016, “How Do Causes Depend on Us? The Many Faces of Perspectivalism”, Synthese, 193(1): 245–267. doi:10.1007/s11229-015-0757-6

Kastner, Ruth E., 2006, “Cramer’s Transactional Interpretation and Causal Loop Problems”, Synthese, 150(1): 1–14. doi:10.1007/s11229-004-6264-9
–––, 2013, The Transactional Interpretation of Quantum Mechanics: The Reality of Possibility, Cambridge: Cambridge University Press. doi:10.1017/CBO9780511675768

Kochen, Simon and E.P. Specker, 1967, “The Problem of Hidden Variables in Quantum Mechanics”, Journal of Mathematics and Mechanics, 17(1): 59–87.

Leifer, Matthew Saul, 2014, “Is the Quantum State Real? An Extended Review of ψ-Ontology Theorems”, Quanta, 3(1): 67. doi:10.12743/quanta.v3i1.22

Leifer, Matthew S. and Matthew F. Pusey, 2017, “Is a Time Symmetric Interpretation of Quantum Theory Possible without Retrocausality?”, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 473(2202): 20160607. doi:10.1098/rspa.2016.0607

Leifer, Matthew S. and Robert W. Spekkens, 2013, “Towards a Formulation of Quantum Theory as a Causally Neutral Theory of Bayesian Inference”, Physical Review A, 88(5): 052130. doi:10.1103/PhysRevA.88.052130

Lewis, G. N., 1926, “The Nature of Light”, Proceedings of the National Academy of Sciences, 12(1): 22–29. doi:10.1073/pnas.12.1.22

Lewis, Peter J., 2013, “Retrocausal Quantum Mechanics: Maudlin’s Challenge Revisited”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(4): 442–449. doi:10.1016/j.shpsb.2013.09.004

Marchildon, Louis, 2006, “Causal Loops and Collapse in the Transactional Interpretation of Quantum Mechanics”., Physics Essays, 19(3): 422–429. doi:10.4006/1.3025811

Maudlin, Tim, 2011, Quantum Non-Locality and Relativity: Metaphysical Intimations of Modern Physics, third edition, Malden, MA: Wiley-Blackwell.

Mellor, D. H., 1998, Real Time II, London: Routledge.

Miller, D.J., 1996, “Realism and Time Symmetry in Quantum Mechanics”, Physics Letters A, 222(1–2): 31–36. doi:10.1016/0375-9601(96)00620-2
–––, 1997, “Conditional Probabilities in Quantum Mechanics from a Time-Symmetric Formulation”, Il Nuovo Cimento B, 112(12): 1577–1592. [Miller 1997 available online]

Näger, Paul M., 2016, “The Causal Problem of Entanglement”, Synthese, 193(4): 1127–1155. doi:10.1007/s11229-015-0668-6

Norsen, Travis, 2011, “John S. Bell’s Concept of Local Causality”, American Journal of Physics, 79(12): 1261–1275. doi:10.1119/1.3630940

Pearl, Judea, 2009, Causality: Models, Reasoning, and Inference, second edition, New York: Cambridge University Press.

Pegg, David T., 2006, “Causality in Quantum Mechanics”, Physics Letters A, 349(6): 411–414. doi:10.1016/j.physleta.2005.09.061
–––, 2008, “Retrocausality and Quantum Measurement”, Foundations of Physics, 38(7): 648–658. doi:10.1007/s10701-008-9224-2

Price, Huw, 1984, “The Philosophy and Physics of Affecting the Past”, Synthese, 61(3): 299–323. doi:10.1007/BF00485056
–––, 1994, “A Neglected Route to Realism about Quantum Mechanics”, Mind, 103(411): 303–336. doi:10.1093/mind/103.411.303
–––, 1996, Time’s Arrow & Archimedes’ Point: New Directions for the Physics of Time, Oxford: Oxford University Press. doi:10.1093/acprof:oso/9780195117981.001.0001
–––, 1997, “Time Symmetry in Microphysics”, Philosophy of Science, 64: S235–S244. doi:10.1086/392603
–––, 2001, “Backward Causation, Hidden Variables and the Meaning of Completeness”, Pramana: Journal of Physics, 56(2–3): 199–209. doi:10.1007/s12043-001-0117-6
–––, 2007, “Causal Perspectivalism”, in Price and Corry 2007: 250–292.
–––, 2008, “Toy Models for Retrocausality”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 39(4): 752–761. doi:10.1016/j.shpsb.2008.05.006
–––, 2012, “Does Time-Symmetry Imply Retrocausality? How the Quantum World Says ‘Maybe’?”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 43(2): 75–83. doi:10.1016/j.shpsb.2011.12.003

Price, Huw and Richard Corry, 2007, Causation, Physics, and the Constitution of Reality: Russell’s Republic Revisited, Oxford: Oxford University Press.

Price, Huw and Brad Weslake, 2010, “The Time‐Asymmetry of Causation”, in The Oxford Handbook of Causation, Helen Beebee, Christopher Hitchcock, and Peter Menzies (eds.), New York: Oxford University Press, chapter 20, 414–443. doi:10.1093/oxfordhb/9780199279739.003.0021

Price, Huw and Ken Wharton, 2015, “Disentangling the Quantum World”, Entropy, 17(12): 7752–7767. doi:10.3390/e17117752
–––, 2021, “Entanglement Swapping and Action at a Distance”, Foundations of Physics, 51: 105. doi:10.1007/s10701-021-00511-3

Pusey, Matthew F., Jonathan Barrett, and Terry Rudolph, 2012, “On the Reality of the Quantum State”, Nature Physics, 8(6): 475–478. doi:10.1038/nphys2309

Quine, W. V., 1951, “Ontology and Ideology”, Philosophical Studies, 2(1): 11–15. doi:10.1007/BF02198233

Rietdijk, C. W., 1978, “Proof of a Retroactive Influence”, Foundations of Physics, 8(7–8): 615–628. doi:10.1007/BF00717585

Ringbauer, Martin, 2017, “On the Reality of the Wavefunction”, in Exploring Quantum Foundations with Single Photons, by Martin Ringbauer, Cham: Springer International Publishing, 85–136. doi:10.1007/978-3-319-64988-7_4

Russell, Bertrand, 1913, “On the Notion of Cause”, Proceedings of the Aristotelian Society, 13(1): 1–26. doi:10.1093/aristotelian/13.1.1

Shrapnel, Sally and Fabio Costa, 2018, “Causation Does Not Explain Contextuality”, Quantum, 2: 63. doi:10.22331/q-2018-05-18-63

Schulman, Lawrence S., 1997, Time’s Arrows and Quantum Measurement, Cambridge: Cambridge University Press. doi:10.1017/CBO9780511622878
–––, 2012, “Experimental Test of the ‘Special State’ Theory of Quantum Measurement”, Entropy, 14(4): 665–686. doi:10.3390/e14040665

Silberstein, Michael, Michael Cifone, and William Mark Stuckey, 2008, “Why Quantum Mechanics Favors Adynamical and Acausal Interpretations Such as Relational Blockworld over Backwardly Causal and Time-Symmetric Rivals”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 39(4): 736–751. doi:10.1016/j.shpsb.2008.07.005

Silberstein, Michael, W.M. Stuckey, and Timothy McDevitt, 2018, Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced, Oxford: Oxford University Press. doi:10.1093/oso/9780198807087.001.0001

Spekkens, Robert W., 2005, “Contextuality for Preparations, Transformations, and Unsharp Measurements”, Physical Review A, 71(5): 052108. doi:10.1103/PhysRevA.71.052108
–––, 2007, “Evidence for the Epistemic View of Quantum States: A Toy Theory”, Physical Review A, 75(3): 032110. doi:10.1103/PhysRevA.75.032110

Spirtes, Peter, Clark N. Glymour, and Richard Scheines, 2000, Causation, Prediction, and Search, second edition, (Adaptive Computation and Machine Learning), Cambridge, MA: MIT Press.

Stuckey, W. M., Michael Silberstein, and Michael Cifone, 2008, “Reconciling Spacetime and the Quantum: Relational Blockworld and the Quantum Liar Paradox”, Foundations of Physics, 38(4): 348–383. doi:10.1007/s10701-008-9206-4

Stuckey, W.M., Michael Silberstein, and Timothy McDevitt, 2015, “Relational Blockworld: Providing a Realist Psi-Epistemic Account of Quantum Mechanics”, International Journal of Quantum Foundations, 1(3): 123–170. [Stuckey et al. 2015 available online]

Sutherland, Roderick Ian, 1983, “Bell’s Theorem and Backwards-in-Time Causality”, International Journal of Theoretical Physics, 22(4): 377–384. doi:10.1007/BF02082904
–––, 1985, “A Corollary to Bell’s Theorem”, Il Nuovo Cimento B, Series 11, 88(2): 114–118. doi:10.1007/BF02728894
–––, 1989, “Implications of a Causality Paradox Related to Bell–s Theorem”, Il Nuovo Cimento B, Series 11, 104(1): 29–33. doi:10.1007/BF02742823
–––, 2008, “Causally Symmetric Bohm Model”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 39(4): 782–805. doi:10.1016/j.shpsb.2008.04.004
–––, 2015, “Lagrangian Description for Particle Interpretations of Quantum Mechanics: Single-Particle Case”, Foundations of Physics, 45(11): 1454–1464. doi:10.1007/s10701-015-9918-1
–––, 2017, “How Retrocausality Helps”, AIP Conference Proceedings, 1841(1): 020001. doi:10.1063/1.4982765

Tetrode, H., 1922, “Über den Wirkungszusammenhang der Welt. Eine Erweiterung der klassischen Dynamik”, Zeitschrift für Physik, 10(1): 317–328. doi:10.1007/BF01332574

Watanabe, Satosi, 1955, “Symmetry of Physical Laws. Part III. Prediction and Retrodiction”, Reviews of Modern Physics, 27(2): 179–186. doi:10.1103/RevModPhys.27.179

Wharton, Ken B., 2007, “Time-Symmetric Quantum Mechanics”, Foundations of Physics, 37(1): 159–168. doi:10.1007/s10701-006-9089-1
–––, 2010a, “A Novel Interpretation of the Klein-Gordon Equation”, Foundations of Physics, 40(3): 313–332. doi:10.1007/s10701-009-9398-2
–––, 2010b, “Time-Symmetric Boundary Conditions and Quantum Foundations”, Symmetry, 2(1): 272–283. doi:10.3390/sym2010272
–––, 2013, “The Universe Is Not a Computer”, New Scientist, 217(2903): 30–31. doi:10.1016/S0262-4079(13)60354-1
–––, 2014, “Quantum States as Ordinary Information”, Information, 5(1): 190–208. doi:10.3390/info5010190
–––, 2016, “Towards a Realistic Parsing of the Feynman Path Integral”, Quanta, 5(1): 1. doi:10.12743/quanta.v5i1.41
–––, 2018, “A New Class of Retrocausal Models”, Entropy, 20(6): 410. doi:10.3390/e20060410

Wharton, Ken B. and Nathan Argaman,, 2020, “Colloquium: Bell’s theorem and locally mediated reformulations of quantum mechanics”, Reviews of Modern Physics, 92(2): 021002. doi:10.1103/RevModPhys.92.021002

Wharton, Ken B., David J. Miller, and Huw Price, 2011, “Action Duality: A Constructive Principle for Quantum Foundations”, Symmetry, 3(3): 524–540. doi:10.3390/sym3030524

Wheeler, John Archibald and Richard Phillips Feynman, 1945, “Interaction with the Absorber as the Mechanism of Radiation”, Reviews of Modern Physics, 17(2–3): 157–181. doi:10.1103/RevModPhys.17.157
–––, 1949, “Classical Electrodynamics in Terms of Direct Interparticle Action”, Reviews of Modern Physics, 21(3): 425–433. doi:10.1103/RevModPhys.21.425

Wigner, Eugene, 1932, “On the Quantum Correction for Thermodynamic Equilibrium”, Physical Review, 40: 033002. doi:10.1088/1367-2630/17/3/033002
–––, 1932, “On the quantum correction for thermodynamic equilibrium”, Physical Review, 40: 749–759.

Wiseman, Howard M. and Eric G. Cavalcanti, 2017, “Causarum Investigatio and the Two Bell’s Theorems of John Bell”, in Quantum [Un]Speakables II: Half a Century of Bell’s Theorem, Reinhold Bertlmann and Anton Zeilinger (eds.), Cham: Springer International Publishing, 119–142. doi:10.1007/978-3-319-38987-5_6

Wood, Christopher J and Robert W Spekkens, 2015, “The Lesson of Causal Discovery Algorithms for Quantum Correlations: Causal Explanations of Bell-Inequality Violations Require Fine-Tuning”, New Journal of Physics, 17(3): 033002. doi:10.1088/1367-2630/17/3/033002

Woodward, James, 2003, Making Things Happen: A Theory of Causal Explanation, New York: Oxford University Press. doi:10.1093/0195155270.001.0001
–––, 2007, “Causation with a Human Face”, in Price and Corry 2007: Chapter 4, pp. 66–105.